题目内容
19．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}+1\\;-1＜x≤0}\\{xsin\frac{1}{x}+a\\;0＜x＜1}\\{2x+b\\;1≤x＜2}\end{array}\right.$在点x=0，x=1处的极限是存在，求a，b？分析 利用函数关系式求解$\underset{lim}{{x}^{-}→0}$（xsin$\frac{1}{x}+a$）=f（0）=2，$\underset{lim}{x→0}$=$\frac{sin\frac{1}{x}}{\frac{1}{x}}$=0，得出a，再求解b即可．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{{e}^{x}+1\\;-1＜x≤0}\\{xsin\frac{1}{x}+a\\;0＜x＜1}\\{2x+b\\;1≤x＜2}\end{array}\right.$在点x=0，x=1处的极限是存在，
∴$\underset{lim}{{x}^{-}→0}$（xsin$\frac{1}{x}+a$）=f（0）=2，
∵$\underset{lim}{x→0}$=$\frac{sin\frac{1}{x}}{\frac{1}{x}}$=0，
∴a=2，
∵f（1）=2+b，$\underset{lim}{{x}^{+}→1}$=sin1+2=f（1）=2+b，
∴b=sin1．
点评 本题简单的考察了极限的概念，运算，理解左极限，右极限的概念，属于容易题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
9．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在某一周期内的图象时，列表并填入了部分数据，如表：
（Ⅰ）根据如表求出函数f（x）的解析式；
（Ⅱ）设△ABC的三内角A，B，C的对边分别为a，b，c，且f（A）=$\sqrt{3}$，a=3，S为△ABC的面积，求S+3$\sqrt{3}$cosBcosC的最大值．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | x1 | $\frac{π}{3}$ | x2 | $\frac{7π}{3}$ | x3 |
| y | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
（Ⅱ）设△ABC的三内角A，B，C的对边分别为a，b，c，且f（A）=$\sqrt{3}$，a=3，S为△ABC的面积，求S+3$\sqrt{3}$cosBcosC的最大值．
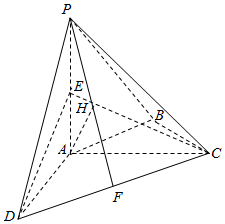如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BCA=45°，AP=AD=AC=2，E、F、H分别为PA、CD、PF的中点．
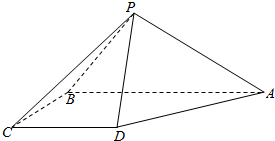如图，四棱锥P-ABCD中，平面PAB⊥平面ABCD，底面ABCD为直角梯形，AB=2CD=2BC=2，AB∥CD，AB⊥BC，△PAB为等腰直角三角形且PA⊥PB．