题目内容
10.函数f(x)=3-x+x2-4的零点个数是2.分析 函数f(x)=3-x+x2-4的零点个数可化为函数y=3-x与y=4-x2的图象的交点的个数;从而作图滶解即可.
解答 解:函数f(x)=3-x+x2-4的零点个数可化为方程3-x=4-x2的解的个数;
即函数y=3-x与y=4-x2的图象的交点的个数;
作函数y=3-x与y=4-x2的图象如下, ,
,
故函数y=3-x与y=4-x2的图象共有2个交点,
故答案为:2.
点评 本题考查了函数的零点与方程的根的关系应用及数形结合的思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.一个长方体底面为正方形且边长为4,高为h,若这个长方体能装下8个半径为1的小球和一个半径为2的大球,则h的最小值为( )
| A. | 8 | B. | 2+2$\sqrt{7}$ | C. | 2+2$\sqrt{5}$ | D. | 6 |
18.已知椭圆的焦点是F1、F2,P是椭圆的一个动点,如果M是线段F1P的中点,则动点M的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线的一支 | D. | 抛物线 |
5.若集合A=[2,3],B={x|x2-5x+6=0|,则A∩B=( )
| A. | {2,3} | B. | ∅ | C. | 2 | D. | [2,3] |
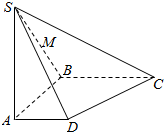 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=∠DAB=90°,SA⊥平面ABCD,SA=AB=BC=2,AD=1,M为SB的中点,过点M、A、D的截面MADN交SC于点N.
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=∠DAB=90°,SA⊥平面ABCD,SA=AB=BC=2,AD=1,M为SB的中点,过点M、A、D的截面MADN交SC于点N.