题目内容
16.已知a∈R,则“a<0”是“函数f(x)=|x(ax+1)|在(-∞,0)上是减函数”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
分析 对a分类讨论,利用二次函数的单调性、绝对值函数的意义即可得出.
解答 解:a=0时,函数f(x)=|x(ax+1)|=|x|在(-∞,0)上是减函数.
a≠0时,f(x)=|a$(x+\frac{1}{2a})^{2}$-$\frac{1}{4a}$|,若函数f(x)=|x(ax+1)|在(-∞,0)上是减函数,则-$\frac{1}{2a}$≥0,解得a<0.
因此“a<0”是“函数f(x)=|x(ax+1)|在(-∞,0)上是减函数”的充分不必要条件.
故选:A.
点评 本题考查了简易逻辑的判定方法、二次函数的单调性、绝对值函数的意义、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
7.用0,1,2,…,299给300名高三学生编号,并用系统抽样的方法从中抽取15名学生的数学成绩进行质量分析,若第一组抽取的学生的编号为8,则第三组抽取的学生编号为( )
| A. | 20 | B. | 28 | C. | 40 | D. | 48 |
4.函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )
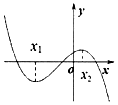

| A. | a>0,b>0,c>0,d<0 | B. | a>0,b>0,c<0,d<0 | C. | a<0,b<0,c>0,d>0 | D. | a>0,b>0,c>0,d>0 |
8.如图是总体密度曲线,下列说法正确的是( )
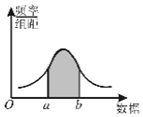

| A. | 组距越大,频率分布折线图越接近于它 | |
| B. | 样本容量越小,频率分布折线图越接近于它 | |
| C. | 阴影部分的面积代表总体在(a,b)内取值的百分比 | |
| D. | 阴影部分的平均高度代表总体在(a,b)内取值的百分比 |
5.设数列{an}满足a1=a,an+1=$\frac{a_n^2-2}{{{a_n}+1}}$(n∈N),若数列{an}是常数列,则a=( )
| A. | -2 | B. | -1 | C. | 0 | D. | (-1)n |
6.已知复数z的实部为-1,虚部为2,则$\frac{5i}{\overline z}$对应的点位于( )
| A. | 第四象限 | B. | 第一象限 | C. | 第三象限 | D. | 第二象限 |
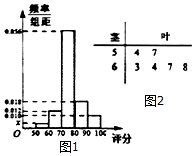 某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.
某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.