题目内容
10.不共线的非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{b}$|=|-2$\overrightarrow{a}$|,则向量2$\overrightarrow{a}$+$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 利用平面向量的数量积为0,可求出两向量的夹角为$\frac{π}{2}$.
解答 解:∵|$\overrightarrow{b}$|=|-2$\overrightarrow{a}$|=2|$\overrightarrow{a}$|,
∴(2$\overrightarrow{a}$+$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=4${\overrightarrow{a}}^{2}$-${\overrightarrow{b}}^{2}$=4${|\overrightarrow{a}|}^{2}$-4${|\overrightarrow{a}|}^{2}$=0,
∴向量2$\overrightarrow{a}$+$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为$\frac{π}{2}$.
故选:D.
点评 本题考查了平面向量量积公式,考查学生的计算能力,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
1.计算$\int_0^4{|{x-2}|dx}$的值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 14 |
5.在一次抽奖活动中,8张奖券中有一、二、三等奖各1张,其余5张无奖.甲、乙、丙、丁四名顾客每人从中抽取2张,则不同的获奖情况有( )
| A. | 24种 | B. | 36种 | C. | 60种 | D. | 96种 |
15.已知 f(x)=$\frac{a-{2}^{x}}{1+{2}^{x}}$(a∈R)是奇函数,且实数k满足f(2k-1)<$\frac{1}{3}$,则k的取值范围是( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
2.已知sin(α+$\frac{π}{3}$)+sinα=-$\frac{4\sqrt{3}}{5}$.-$\frac{π}{2}$<α<0,则sin(-α+$\frac{5π}{6}$)等于( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
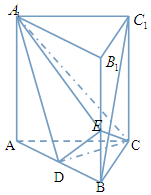 如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.