题目内容
已知函数
(1)求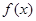 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)已知 是
是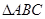 三边长,且
三边长,且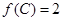 ,
,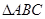 的面积
的面积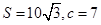 .求角
.求角 及
及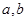 的值.
的值.
(1) ,
, ;(2)
;(2) 或a=5,b=8.
或a=5,b=8.
解析试题分析:(2)由函数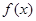 的结构形式可得,应用正弦的和差的展开式公式,以及余弦的二倍角逆运算公式,将函数
的结构形式可得,应用正弦的和差的展开式公式,以及余弦的二倍角逆运算公式,将函数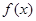 化简,再通过应用角和差的逆运算公式,将函数
化简,再通过应用角和差的逆运算公式,将函数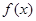 化简,即可求得最小正周期,和单调递增区间.
化简,即可求得最小正周期,和单调递增区间.
(2)在三角形中,根据(Ⅰ)的结论,求出角C.又由已知面积、c边长这三个条件即可解三角形,及求出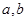 的值.本小题在解关于
的值.本小题在解关于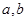 的方程组时要用到整体的思想.
的方程组时要用到整体的思想.
试题解析:(Ⅰ)
 Com]
Com]


 ,
, ,
,
函数 的递增区间是
的递增区间是
(2) 或a=5,b=8
或a=5,b=8
考点:1.三角形函数的恒等变换公式.2.解三角形的知识.3.整体的数学思想.

练习册系列答案
相关题目
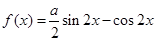 的图象过点
的图象过点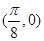 .
.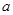 的值;
的值; 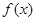 的最小正周期及最大值.
的最小正周期及最大值. ,求cosθ的值.
,求cosθ的值.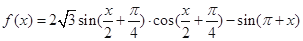 .
. 的最小正周期.
的最小正周期.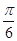 个单位,得到函数
个单位,得到函数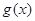 的图象,求函数
的图象,求函数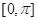 上的值域.
上的值域.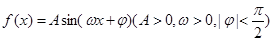 的部分图象如图所示。
的部分图象如图所示。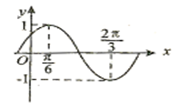
 的最小正周期及解析式;
的最小正周期及解析式;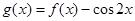 ,求函数
,求函数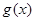 在区间
在区间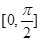 上的最小值.
上的最小值.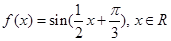 。
。 的单调递减区间;
的单调递减区间;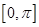 上的最大值及最小值;
上的最大值及最小值;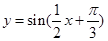 的图象作怎样的变换可得到
的图象作怎样的变换可得到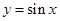 的图象?
的图象?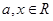 ,函数
,函数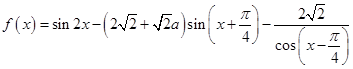 .
.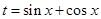 ,将函数
,将函数 表示为关于
表示为关于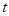 的函数
的函数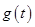 ,求
,求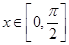 ,不等式
,不等式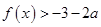 都成立,求实数
都成立,求实数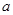 的取值范围.
的取值范围. cos4x.
cos4x. ,π),且f(α)=
,π),且f(α)=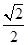 ,求α的值.
,求α的值. ,且角α在第四象限,计算:
,且角α在第四象限,计算: (n∈Z).
(n∈Z).