题目内容
已知函数f(x)=(2cos2x-1)sin2x+ cos4x.
cos4x.
(1)求f(x)的最小正周期及最大值;
(2)若α∈( ,π),且f(α)=
,π),且f(α)=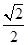 ,求α的值.
,求α的值.
(1) f(x)的最小正周期为 ,最大值为
,最大值为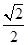 (2)
(2) 
解析解:(1)因为f(x)=(2cos2x-1)sin2x+ cos4x
cos4x
=cos2xsin2x+ cos4x
cos4x
= (sin4x+cos4x)
(sin4x+cos4x)
=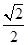 sin(4x+
sin(4x+ ),
),
所以f(x)的最小正周期为 ,最大值为
,最大值为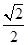 .
.
(2)因为f(α)=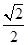 ,所以sin(4α+
,所以sin(4α+ )=1.
)=1.
因为α∈( ,π),
,π),
所以4α+ ∈(
∈( ,
, ).
).
所以4α+ =
= .故α=
.故α= .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,函数
,函数 .
. ,x为某三角形的内角,求
,x为某三角形的内角,求 时x的值;
时x的值; ,当函数
,当函数 取最大值时,求cos2x的值.
取最大值时,求cos2x的值.
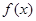 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 是
是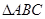 三边长,且
三边长,且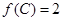 ,
,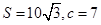 .求角
.求角 及
及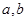 的值.
的值.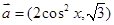 ,
,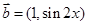 ,函数
,函数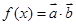 .
. 的最小正周期;
的最小正周期;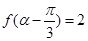 ,
,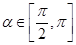 ,求
,求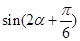 的值.
的值.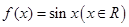 与
与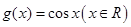 .
.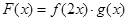 ,有下列结论:①
,有下列结论:①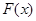 是奇函数;②
是奇函数;②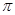 ;③
;③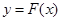 的图象关于点
的图象关于点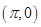 对称;④
对称;④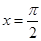 对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)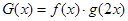 ,求满足
,求满足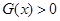 的
的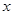 的取值范围;
的取值范围;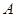 ,函数
,函数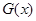 的值域为
的值域为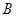 ,试判断集合
,试判断集合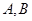 之间的关系.
之间的关系.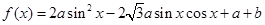 定义域为
定义域为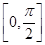 ,值域为[-5,1],求实数
,值域为[-5,1],求实数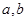 的值。
的值。 ),f(x)=a·b.
),f(x)=a·b.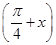 -
- cos 2x-1(x∈R).
cos 2x-1(x∈R).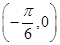 对称,且t∈(0,π),求t的值;
对称,且t∈(0,π),求t的值;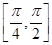 ,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.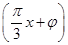 ,x∈R,A>0,0<φ<
,x∈R,A>0,0<φ<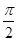 ,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).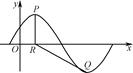
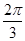 ,求A的值.
,求A的值.