题目内容
16.在平面直角坐标系中,直线l的参数方程为$\left\{\begin{array}{l}x=1+t\\ y=t-3\end{array}\right.$(t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为$ρ=\frac{2cosθ}{{{{sin}^2}θ}}$.(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若直线l与曲线C相交于A,B两点,求弦长|AB|.
分析 (1)利用三种方程的互化方法,求曲线C的直角坐标方程和直线l的普通方程;
(2)将直线l的方程y=x-4代入曲线C的普通方程y2=2x,得x2-10x+16=0,利用韦达定理及弦长公式求弦长|AB|.
解答 解:(1)由曲线C的极坐标方程是:$ρ=\frac{2cosθ}{{{{sin}^2}θ}}$,得ρ2sin2θ=2ρcosθ.
∴由曲线C的直角坐标方程是:y2=2x.由直线l的参数方程$\left\{\begin{array}{l}x=1+t\\ y=t-3\end{array}\right.$,得t=3+y
代入x=1+t中消去t得:x-y-4=0,所以直线l的普通方程为:x-y-4=0-------(5分)
(2)设A(x1,y1),B(x2,y2),
将直线l的方程y=x-4代入曲线C的普通方程y2=2x,得x2-10x+16=0,所以x1+x2=10,x1x2=16,
∴$|{AB}|=\sqrt{1+1}|{{x_1}-{x_2}}|=\sqrt{2}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=6\sqrt{2}$,
点评 本题考查三种方程的互化,考查直线与抛物线位置关系,考查弦长公式,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
6.若函数$f(x)=asinx-\frac{{3\sqrt{3}}}{2}cosx+2$,且$f(\frac{π}{2})=\frac{7}{2}$,则函数f(x)的一条对称轴的方程为( )
| A. | $x=\frac{2π}{3}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{5π}{6}$ | D. | $x=\frac{π}{6}$ |
11.过点(0,3)且与直线2x+y-5=0垂直的直线方程为( )
| A. | 2x+y-3=0 | B. | x+2y-6=0 | C. | x-2y+6=0 | D. | 2x-y+3=0 |

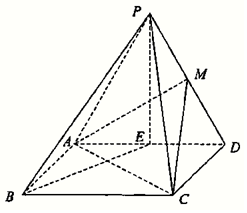 如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.
 B.
B. C.
C. D.
D.
 满足
满足 则
则 的最大值等于( )
的最大值等于( ) B.
B. C.
C. D.
D.