题目内容
18.已知p:“直线x+y-m=0与圆(x-1)2+y2=1相交”;q:“方程mx2-2x+1=0有实数解”.若“p∨q”为真,“¬q”为假,则实数m的取值范围.分析 分别求出p,q为真时的m的范围,根据p∨q”为真,“¬q”为假,得到q真即可求出m的范围.
解答 解:∵直线x+y-m=0与圆(x-1)2+y2=1相交,
∴(1,0)到x+y-m=0的距离小于1,
即$\frac{|1+0-m|}{\sqrt{2}}$<1,解得:1-$\sqrt{2}$<1+$\sqrt{2}$,
故p:m∈(1-$\sqrt{2}$,1+$\sqrt{2}$);
m=0时,方程mx2-2x+1=0有实数解,
m≠0时,若方程mx2-2x+1=0有实数解,
则△=4-4m≥0,解得:m≤1,
故q:m∈(-∞,1],
若“p∨q”为真,“¬q”为假,
则p真q真或p假q真,
故m∈(-∞,1].
点评 本题考查了直线和圆的关系,考查方程根的问题以及复合命题的判断,是一道中档题.

练习册系列答案
相关题目
8.若一个球的半径为1,则它的表面积是( )
| A. | 4π | B. | 2π | C. | π | D. | $\frac{3π}{4}$ |
9.等差数列{an}的首项为a,公差为1,数列{bn}满足bn=$\frac{{a}_{n}}{{a}_{n}+1}$.若对任意n∈N*,bn≤b6,则实数a的取值范围是( )
| A. | (-8,-6) | B. | (-7,-6) | C. | (-6,-5) | D. | (6,7) |
6.若函数$f(x)=asinx-\frac{{3\sqrt{3}}}{2}cosx+2$,且$f(\frac{π}{2})=\frac{7}{2}$,则函数f(x)的一条对称轴的方程为( )
| A. | $x=\frac{2π}{3}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{5π}{6}$ | D. | $x=\frac{π}{6}$ |
3.设x∈R,向量$\overrightarrow{a}$=(3,x),$\overrightarrow{b}$=(-1,1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$|=( )
| A. | 6 | B. | 4 | C. | $3\sqrt{2}$ | D. | 3 |
10.已知集合A={0,1,2},B={x|1<x<4},则集合A∩B=( )
| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
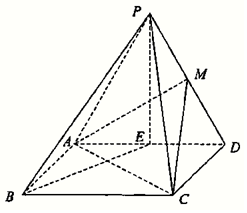 如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.