题目内容
14.对于函数$f(x)=\frac{1}{1-x}$,定义${f_1}(x)=f(x),{f_{n+1}}(x)=f[{{f_n}(x)}]\;\;(n∈{N^*})$.已知偶函数g(x)的定义域为(-∞,0)∪(0,+∞),g(1)=0;当x>0,且x≠1时,g(x)=f2015(x).(1)求f2(x),f3(x),f4(x),并求出函数y=g(x)的解析式;
(2)若存在实数a,b(a<b)使得函数g(x)在[a,b]上的值域为[mb,ma],求实数m的取值范围.
分析 (1)根据函数关系进行求解即可.
(2)根据函数奇偶性的性质,结合函数的值域关系进行求解即可.
解答 解:(1)因为${f_1}(x)=f(x)=\frac{1}{1-x}\;({x≠1}),\;\;故$${f_2}(x)=f[{{f_1}(x)}]=\frac{1}{{1-\frac{1}{1-x}}}=1-\frac{1}{x}\;({x≠0,x≠1})$,$\begin{array}{l}{f_3}(x)=f[{{f_2}(x)}]=\frac{1}{{1-(1-\frac{1}{x})}}=x\;(x≠0,x≠1),\;\;\\{f_4}(x)=f[{{f_3}(x)}]=\frac{1}{1-x}\;\;(x≠0,x≠1),…(3分)\end{array}$
故对任意的n∈N•,有f3n+i(x)=fi(x)(i=2,3,4),
于是${f_{2015}}(x)={f_{3×671+2}}(x)={f_2}(x)=1-\frac{1}{x}\;(x≠0,x≠1)$;$故当\;x>0,x≠1\;时,g(x)={f_{2015}}(x)=1-\frac{1}{x}$.$又g(1)=0,故当\;x>0\;时,g(x)=1-\frac{1}{x}$.
由g(x)为偶函数,$当\;x<0\;时,-x>0,g(x)=g(-x)=1-\frac{1}{-x}=1+\frac{1}{x}$.${因此}g(x)=\left\{\begin{array}{l}1+\;\frac{1}{x},\;x<0\\ 1-\frac{1}{x},\;x>0.\end{array}\right.=1-\;\frac{1}{|x|}$.…(6分)
(2)由于y=g(x)的定义域为(-∞,0)∪(0,+∞),
又a<b,mb<ma,可知a与b同号,且m<0;进而g(x)在[a,b]递减,且a<b<0.…(8分)
函数y=g(x)的图象,如图所示.由题意,有$\left\{\begin{array}{l}g(a)=1+\;\frac{1}{a}=ma\\ g(b)=1+\;\frac{1}{b}=mb\end{array}\right.$…(10分)
故a,b是方程$1+\;\frac{1}{x}=m\;x$的两个不相等的负实数根,即方程mx2-x-1=0在(-∞,0)上有
两个不相等的实根,于是$\begin{array}{l}\left\{\begin{array}{l}△=1+4m>0\\ a+b=\;\frac{1}{m}<0\\ ab=-\;\frac{1}{m}>0\end{array}\right.\\?-\frac{1}{4}<m<0.\end{array}$…(12分)
综合上述,得:实数m的取值范围为$({-\frac{1}{4},0})$.…(14分)
注:若采用数形结合,得出直线y=mx与曲线$y=1+\;\frac{1}{x}\;(x<0)$有两个不同交点,并进行求解也可.
点评 本题主要考查函数解析式的求解以及函数奇偶性的应用,考查学生的运算和推理能力.

| 男公务员 | 女公务员 | |
| 生二胎 | 40 | 20 |
| 不生二胎 | 20 | 20 |
(2)把以上频率当概率,若从社会上随机抽取3位30到40岁的男公务员,记其中生二胎的人数为X,求随机变量X的分布列,数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
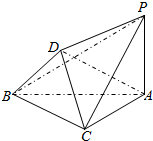 如图,在多面体PABCD中,△ABC是边长为2的正三角形,BD=DC=$\sqrt{3}$,AD=$\sqrt{5}$,PA⊥平面ABC.
如图,在多面体PABCD中,△ABC是边长为2的正三角形,BD=DC=$\sqrt{3}$,AD=$\sqrt{5}$,PA⊥平面ABC. 如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.
如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$. 如图,已知四边形ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3,PB的中点E,求异面直线AE与PC所成角的大小.(用反三角表示)
如图,已知四边形ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3,PB的中点E,求异面直线AE与PC所成角的大小.(用反三角表示)