题目内容
13．计算${∫}_{1}^{2}$（x+$\frac{1}{x}$）dx的值为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{3}{2}$+ln2 | C． | $\frac{5}{2}$+ln2 | D． | 3+ln2 |
分析 找出被积函数的原函数，利用微积分基本定理求值．
解答 解：${∫}_{1}^{2}$（x+$\frac{1}{x}$）dx=$（\frac{1}{2}{x}^{2}+lnx）{|}_{1}^{2}$=2+ln2-$\frac{1}{2}$=ln2+$\frac{3}{2}$；
故选B．
点评 本题考查了定积分的计算；属于基础题．
练习册系列答案
考前必练系列答案
相关题目
3．若集合A={-3，-1，0，2，4}，集合B={x|x＞log23}，则A∩（∁RB）等于（ ）
| A． | {2，4} | B． | {-3，-1} | C． | {-3，-1，0} | D． | {0，2，4} |
1．
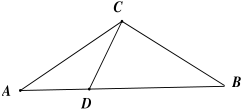如图，在等腰△ABC中，∠C=120°，DA=DC，过顶点C在∠ACB内部作一条射线CM，与线段AB交于点M，则AM＜$\frac{{\sqrt{3}}}{3}$AC的概率为（ ）
如图，在等腰△ABC中，∠C=120°，DA=DC，过顶点C在∠ACB内部作一条射线CM，与线段AB交于点M，则AM＜$\frac{{\sqrt{3}}}{3}$AC的概率为（ ）| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{4}$ |
5．已知全集U={x|x＞0}，M={x|x＞1}，则∁UM=（ ）
| A． | {x|x≤1} | B． | {x|0＜x≤1} | C． | {x|x≥0} | D． | {x|x≤0或x＞1} |