已知sinα=$\frac{1}{3}$.求$\frac{si{n}^{2}α}{co{s}^{2}α}$+sinα的值．题目和参考答案——青夏教育精英家教网—

题目内容

19．已知sinα=$\frac{1}{3}$，求$\frac{si{n}^{2}α}{co{s}^{2}α}$+sinα的值．

分析由条件利用同角三角函数的基本关系，求得要求式子的值．

解答解：∵sinα=$\frac{1}{3}$，∴$\frac{si{n}^{2}α}{co{s}^{2}α}$+sinα=$\frac{{sin}^{2}α}{1{-sin}^{2}α}$+sinα=$\frac{\frac{1}{9}}{1-\frac{1}{9}}$+$\frac{1}{3}$=$\frac{11}{24}$．

点评本题主要考查同角三角函数的基本关系的应用，属于基础题．

练习册系列答案

10．（log₉4）（log₂27）=（　　）

7．已知数列{a_n}满足a_n+a_n-1=（-1）${\;}^{\frac{n（n+1）}{2}}$n，S_n是其前n项和，若 S₂₀₁₇=-1007-b，且a₁b＞0，则$\frac{1}{{a}_{1}}$+$\frac{2}{b}$的最小值为（　　）

14．已知{a_n}是公差不为零的等差数列，a₁=1，且a₁，a₃，a₉成等比数列．求数列{a_n}的通项公式．

4．已知抛物线C：x²=12y的焦点为F，准线为l，P∈l，Q是线段PF与C的一个交点，若|PF|=3|FQ|．则|FQ|=（　　）

11．下列关于函数 y=ln|x|的叙述正确的是（　　）

	A．	奇函数，在（0，+∞）上是增函数		B．	奇函数，在（0，+∞）上是减函数
	C．	偶函数，在（0，+∞）上是减函数		D．	偶函数，在（0，+∞）上是增函数

8．

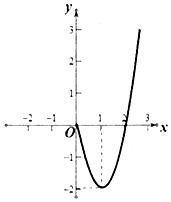已知函数y=f（x）定义在实数集R上的奇函数，当x≥0时，函数y=f（x）的图象如图所示（抛物线的一部分）．
（1）在原图上画出x＜0时函数y=f（x）的示意图；
（2）求函数y=f（x）的解析式（不要求写出解题过程）；
（3）写出函数y=|f（x）|的单调递增区间（不要求写出解题过程）．

9．圆（x-3）²+（y+4）²=1关于y²=8x轴对称的圆的方程是（　　）

试题分类