题目内容
9．求函数y=log2（-2x2+5x+3）（-$\frac{1}{2}$＜x＜3）的单调减区间．分析 先求出函数的定义域，然后利用复合函数的单调性确定函数f（x）的单调递减区间．
解答 解：∵-$\frac{1}{2}$＜x＜3，∴-2x2+5x+3＞0，
内函数t=-2x2+5x+3在（$\frac{5}{4}，3$）上为减函数，外函数y=log2t为增函数，
∴函数y=log2（-2x2+5x+3）（-$\frac{1}{2}$＜x＜3）的单调减区间为（$\frac{5}{4}，3$）．
点评 本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”，是中档题．
练习册系列答案
相关题目
20．若（1+x）4=a0+a1x+a2x2+a3x3+a4x4，则a1+a2+a3+a4的值为（ ）
| A． | 0 | B． | 15 | C． | 16 | D． | 17 |
4．
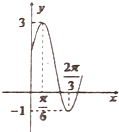如图所示，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分，则函数解析式是（ ）
如图所示，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分，则函数解析式是（ ）| A． | $y=2sin（2x+\frac{π}{6}）+1$ | B． | $y=sin（2x+\frac{π}{3}）+1$ | C． | $y=2sin（\frac{1}{2}x+\frac{π}{6}）+2$ | D． | $y=sin（2x+\frac{π}{3}）+2$ |