题目内容
5.已知点A(1,$\sqrt{3}$)在圆C:x2+y2=4上,则过点A的圆C的切线方程x+$\sqrt{3}$y-4=0.分析 直接利用圆上的点的切线方程,求出即可.
解答 解:因为(1,$\sqrt{3}$)是圆x2+y2=4上的点,
所以它的切线方程为:x+$\sqrt{3}$y=4,
即:x+$\sqrt{3}$y-4=0,
故答案为:x+$\sqrt{3}$y-4=0.
点评 本题考查圆的切线方程,判断点在圆上是解题的关键.圆上的点(x0,y0)的切线方程为:xx0+yy0=R2,值得注意圆的切线方程的应用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
10.已知不等式x2-2ax+a>0(x∈R)恒成立,则不等式a2x+1<a${\;}^{{x}^{2}+2x-3}$<1的解集是( )
| A. | (1,2) | B. | (-$\frac{1}{2}$,2) | C. | (-2,2) | D. | (-3,2) |
15.阅读如右图所示的程序框图,则输出的值是( )


| A. | 6 | B. | 18 | C. | 27 | D. | 124 |
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥平面AB1C1,AA1=1,底面△ABC是边长为2的正三角形,则三棱锥A-A1B1C1的体积为$\sqrt{2}$.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥平面AB1C1,AA1=1,底面△ABC是边长为2的正三角形,则三棱锥A-A1B1C1的体积为$\sqrt{2}$.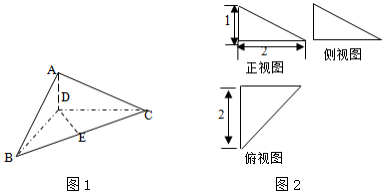
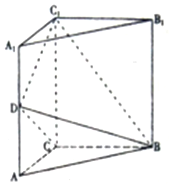 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=$\frac{1}{2}A{A_1}$=2,点D是棱AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=$\frac{1}{2}A{A_1}$=2,点D是棱AA1的中点.