题目内容
1．若（9x-$\frac{1}{3\sqrt{x}}$）n（n∈N*）的展开式中第2项的二项式系数为9，则其展开式中的常数项为（ ）| A． | -84 | B． | -252 | C． | 252 | D． | 84 |
分析 先求出二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得展开式中的常数项的值．
解答 解：由题意可得${C}_{n}^{1}$=9，∴n=9，故（9x-$\frac{1}{3\sqrt{x}}$）n即（9x-$\frac{1}{3\sqrt{x}}$）9，
故（9x-$\frac{1}{3\sqrt{x}}$）9的展开式的通项公式为Tr+1=${C}_{9}^{r}$•${（-\frac{1}{3}）}^{r}$•99-r•${x}^{9-\frac{3r}{2}}$，
令9-$\frac{3r}{2}$=0，求得r=6，故其展开式中的常数项为${C}_{9}^{3}$${（\frac{1}{3}）}^{6}$•93=84，
故选：D．
点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．
练习册系列答案
相关题目
11．
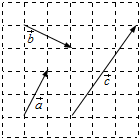如图，在6×6的方格纸中，若起点和终点均在格点的向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$，（x，y∈R），则x+y=（ ）
如图，在6×6的方格纸中，若起点和终点均在格点的向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$，（x，y∈R），则x+y=（ ）| A． | 0 | B． | 1 | C． | 5$\sqrt{5}$ | D． | $\frac{13}{5}$ |
12．已知圆x2+y2=1上两点A、B与坐标原点O恰构成正三角形，则向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的数量积是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 1 | D． | -1 |
9．现定义an=5n+（$\frac{1}{5}$）n，其中n∈{$\frac{1}{10}$，$\frac{1}{5}$，$\frac{1}{2}$，1}，则an取最小值时，n的值为（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{2}$ | D． | 1 |
6．关于函数f（x）=log3（-x）和g（x）=3-x，下列说法中正确的是（ ）
| A． | 都是奇函数 | B． | 都是偶函数 | C． | 函数f（x）的值域为R | D． | 函数g（x）的值域为R |
13．已知PC为球O的直径，A，B是球面上两点，且AB=6，∠APC=∠BPC=$\frac{π}{4}$若球O的表面积为64π，则棱锥A-PBC的体积为（ ）
| A． | $8\sqrt{7}$ | B． | $24\sqrt{7}$ | C． | $\frac{{4\sqrt{3}}}{3}$ | D． | $\frac{{2\sqrt{21}}}{5}$ |
.
时，求不等式
的解集；
的图象与
轴围成的三角形面积大于6，求
的取值范围.