题目内容
11.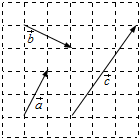 如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,(x,y∈R),则x+y=( )
如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,(x,y∈R),则x+y=( )| A. | 0 | B. | 1 | C. | 5$\sqrt{5}$ | D. | $\frac{13}{5}$ |
分析 根据向量的运算法则以及向量的基本定理进行运算即可.
解答 解:将向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$放入坐标系中,
则向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-1),$\overrightarrow{c}$=(3,4),
∵$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,
∴(3,4)=x(1,2)+y(2,-1),
即$\left\{\begin{array}{l}{x+2y=3}\\{2x-y=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{11}{5}}\\{y=\frac{2}{5}}\end{array}\right.$,
则x+y=$\frac{11}{5}+\frac{2}{5}=\frac{13}{5}$,
故选:D.
点评 本题主要考查向量的分解,利用向量的坐标运算是解决本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
6.设全集U=R,集合M={x|x>1},P={x|x2>1},则下列关系中正确的是( )
| A. | M=P | B. | P?M | C. | M?P | D. | ∁U(M∪P)=∅ |
1.若(9x-$\frac{1}{3\sqrt{x}}$)n(n∈N*)的展开式中第2项的二项式系数为9,则其展开式中的常数项为( )
| A. | -84 | B. | -252 | C. | 252 | D. | 84 |
 某校从参加高三年级期末考试的学生中随机抽取100名学生,将其数学成绩分成五段:[50,70),[70,90),[90,110),[110,130),[130,150],它的频率分布直方图如图所示,则该批学生中成绩不低于90分的人数是65.
某校从参加高三年级期末考试的学生中随机抽取100名学生,将其数学成绩分成五段:[50,70),[70,90),[90,110),[110,130),[130,150],它的频率分布直方图如图所示,则该批学生中成绩不低于90分的人数是65. 如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则$\frac{x}{y}$=$\frac{11}{2}$.
如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则$\frac{x}{y}$=$\frac{11}{2}$.