题目内容
关于x的方程cos2x-sinx+a=0,若0<x≤
时方程有解,则a的取值范围( )
| π |
| 2 |
| A、[-1,1] | ||
| B、(-1,1] | ||
| C、[-1,0] | ||
D、(-∞,-
|
考点:三角函数的最值
专题:计算题,三角函数的图像与性质
分析:cos2x-sinx+a=0⇒a=sinx-cos2x=(sinx+
)2-
;当0<x≤
时,利用正弦函数的单调性可求得-1<(sinx+
)2-
≤1,从而可得a的取值范围.
| 1 |
| 2 |
| 5 |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
解答:
解:∵cos2x-sinx+a=0,
∴a=sinx-cos2x
=sinx-(1-sin2x)
=(sinx+
)2-
;
∵0<x≤
,
∴0<sinx≤1,
∴
<sinx+
≤
,
∴
<(sinx+
)2≤
,
∴-1<(sinx+
)2-
≤1,即-1<a≤1.
∴a的取值范围为(-1,1].
故选:B.
∴a=sinx-cos2x
=sinx-(1-sin2x)
=(sinx+
| 1 |
| 2 |
| 5 |
| 4 |
∵0<x≤
| π |
| 2 |
∴0<sinx≤1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
∴-1<(sinx+
| 1 |
| 2 |
| 5 |
| 4 |
∴a的取值范围为(-1,1].
故选:B.
点评:本题考查三角函数的最值,考查分离变量法的应用,突出考查正弦函数的单调性与配方法,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知集合A={x|y=
},B={x|
≤0},则A∩B=( )
| x+1 |
| x-1 |
| x+1 |
| A、(-1,1] |
| B、[-1,1] |
| C、[1,+∞) |
| D、[0,1] |
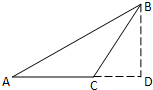 已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若
已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若| AB |
| a |
| AC |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在某市创建全国文明城市工作验收时,国家文明委有关部门对某校高二年级6名学生进行了问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体.如果用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本,则该样本平均数与总体平均数之差的绝对值不超过0.5的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设a,b,c∈R,且a<b,则( )
| A、ac>bc | ||||
B、
| ||||
| C、a2>b2 | ||||
| D、a3<b3 |