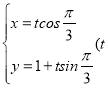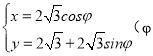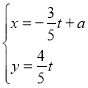题目内容
【题目】已知椭圆![]() :
:![]()
![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() .直线
.直线![]() 交于点
交于点![]() ,倾斜角互补,且直线
,倾斜角互补,且直线![]() 与椭圆
与椭圆![]() 的交点分别为
的交点分别为![]() (点
(点![]() 在点
在点![]() 的右侧).
的右侧).
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:直线![]() 的斜率为定值;
的斜率为定值;
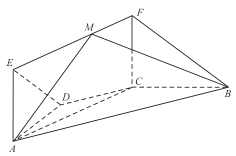
(Ⅲ)在椭圆上是否存在一点![]() ,恰好使得四边形
,恰好使得四边形![]() 为平行四边形,若存在,分别指出此时点
为平行四边形,若存在,分别指出此时点![]() 和
和![]() 的坐标;若不存在,简述理由.
的坐标;若不存在,简述理由.
【答案】(Ⅰ)![]() (Ⅱ)证明见解析(Ⅲ)存在,
(Ⅱ)证明见解析(Ⅲ)存在,![]()
【解析】
(Ⅰ)根据长轴长和离心率即可容易求得![]() ,则椭圆方程可得;
,则椭圆方程可得;
(Ⅱ)由![]() 点在椭圆上,结合
点在椭圆上,结合![]() 的斜率互为相反数,结合韦达定理,即可容易求得
的斜率互为相反数,结合韦达定理,即可容易求得![]() 两点的坐标,即可求证斜率为定值;
两点的坐标,即可求证斜率为定值;
(Ⅲ)根据题意,即可容易求得对应点的坐标.
(Ⅰ)根据题意得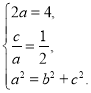 解得
解得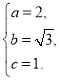
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)易知点![]() 在椭圆
在椭圆![]() 上.
上.
设直线![]()
![]() ,即
,即![]() .
.
令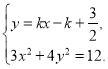
消去![]() 得
得![]() .
.
设![]() ,则
,则![]() .
.
所以![]() .
.
因为直线![]() 和
和![]() 的倾斜角互补,所以直线
的倾斜角互补,所以直线![]()
![]() .
.
设![]() ,同理可得
,同理可得![]() .
.
所以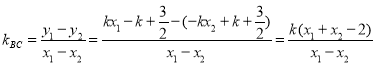
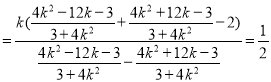 .
.
即直线![]() 的斜率为定值
的斜率为定值![]() .
.
(Ⅲ)存在![]() 符合已知条件,
符合已知条件,
且使得四边形![]() 为平行四边形.
为平行四边形.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目