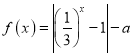Question

【题目】已知点是抛物线：的焦点，点为抛物线的对称轴与其准线的交点，过作抛物线的切线，切点为，若点恰好在以，为焦点的双曲线上，则双曲线的离心率为（ ）

A. B. C. D.

Answer 1

【答案】D

【解析】

根据抛物线的性质，设出直线方程，代入抛物线方程，求得k的值，设出双曲线方程，求得2a＝丨AF2丨﹣丨AF1丨＝（1）p，利用双曲线的离心率公式求得e．

直线F2A的直线方程为：y＝kx，F1（0，），F2（0，），

代入抛物线C：x2＝2py方程，整理得：x2﹣2pkx+p2＝0，

∴△＝4k2p2﹣4p2＝0，解得：k＝±1，

∴A（p，），设双曲线方程为：1，

丨AF1丨＝p，丨AF2丨p，

2a＝丨AF2丨﹣丨AF1丨＝（ 1）p，

2c＝p，

∴离心率e1，

故选：D．