题目内容
【题目】设实数列![]() 满足
满足![]() ,则下面说法正确的是( )
,则下面说法正确的是( )
A.若![]() ,则
,则![]() 前2019项中至少有1010个值相等
前2019项中至少有1010个值相等
B.若![]() ,则当
,则当![]() 确定时,一定存在实数
确定时,一定存在实数![]() 使
使![]() 恒成立
恒成立
C.若![]() ,
,![]() 一定为等比数列
一定为等比数列
D.若![]() ,则当
,则当![]() 确定时,一定存在实数
确定时,一定存在实数![]() 使
使![]() 恒成立
恒成立
【答案】D
【解析】
对于A,由抽屉原理可知前2019项中至少有1009个值相等,即其中的偶数项都为0;对于B,由不动点理论知,![]() 所对应的特征函数
所对应的特征函数![]() ,当a确定时,数列
,当a确定时,数列![]() 单调递增无上界;对于C,若
单调递增无上界;对于C,若![]() ,不排除数列的项可以为0,所以
,不排除数列的项可以为0,所以![]() 不为等比数列;对于D,由数学归纳法能证明:若
不为等比数列;对于D,由数学归纳法能证明:若![]() ,则当a确定时,一定存在实数M使
,则当a确定时,一定存在实数M使![]() 恒成立.
恒成立.
对于A,![]() ,
,![]() ,
,
![]() 由抽屉原理可知前2019项中至少有1009个值相等,即其中的偶数项都为0,故A错误;
由抽屉原理可知前2019项中至少有1009个值相等,即其中的偶数项都为0,故A错误;
对于B,由不动点理论知,![]() 所对应的特征函数
所对应的特征函数![]() ,
,
![]() 当a确定时,数列
当a确定时,数列![]() 单调递增无上界,故B错误;
单调递增无上界,故B错误;
对于C,若![]() ,则数列的项可以为0,所以
,则数列的项可以为0,所以![]() 不为等比数列,故C错误;
不为等比数列,故C错误;
对于D,由数学归纳法知,当![]() 时,
时,![]() ,
,![]() ,使得
,使得![]() 成立;
成立;
假设![]() ,
,![]() 成立,则
成立,则![]() ,
,![]() ,
,
![]() ,
,
![]() 对应的
对应的![]() 存在,
存在,
![]() 若
若![]() ,则当a确定时,一定存在实数M使
,则当a确定时,一定存在实数M使![]() 恒成立,故D正确.
恒成立,故D正确.
故选:D.

 名校课堂系列答案
名校课堂系列答案【题目】某芯片公司为制定下一年的研发投入计划,需了解年研发资金投入量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①
(单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①![]() ,②
,②![]() ,其中
,其中![]() 均为常数,
均为常数,![]() 为自然对数的底数.
为自然对数的底数.
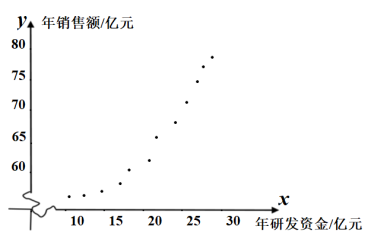
现该公司收集了近12年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,
的数据,![]() ,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令
,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令![]()
![]()
![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)设![]() 和
和![]() 的相关系数为
的相关系数为![]() ,
,![]() 和
和![]() 的相关系数为
的相关系数为![]() ,请从相关系数的角度,选择一个拟合程度更好的模型;
,请从相关系数的角度,选择一个拟合程度更好的模型;
(2)(i)根据(1)的选择及表中数据,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(ii)若下一年销售额![]() 需达到90亿元,预测下一年的研发资金投入量
需达到90亿元,预测下一年的研发资金投入量![]() 是多少亿元?
是多少亿元?
附:①相关系数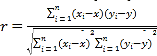 ,回归直线
,回归直线![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: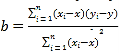 ,
,![]() ;
;
② 参考数据:![]() ,
,![]() ,
,![]() .
.