题目内容
17.若($\sqrt{x}$-$\frac{3}{x}$)n的展开式中各项系数绝对值之和为1024,则展开式中x的系数为( )| A. | 15 | B. | 10 | C. | -15 | D. | -10 |
分析 ($\sqrt{x}$-$\frac{3}{x}$)n的展开式中各项系数绝对值之和与$(\sqrt{x}+\frac{3}{x})^{n}$的展开式中各项系数之和相等.对$(\sqrt{x}+\frac{3}{x})^{n}$,令x=1,则其展开式中各项系数之和=4n.解得n,再利用通项公式即可得出.
解答 解:($\sqrt{x}$-$\frac{3}{x}$)n的展开式中各项系数绝对值之和与$(\sqrt{x}+\frac{3}{x})^{n}$的展开式中各项系数之和相等.
对$(\sqrt{x}+\frac{3}{x})^{n}$,令x=1,则其展开式中各项系数之和=4n.
∴4n=1024,解得n=5.
∴$(\sqrt{x}-\frac{3}{x})^{5}$的通项公式Tr+1=${∁}_{5}^{r}$$(\sqrt{x})^{5-r}$$(-\frac{3}{x})^{r}$=(-3)r${∁}_{5}^{r}$${x}^{\frac{5}{2}-\frac{3r}{2}}$,
令$\frac{5}{2}-\frac{3r}{2}$=1,解得r=1.
∴展开式中x的系数=-3×${∁}_{5}^{1}$=-15.
故选:C.
点评 本题考查了二项式定理的性质及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
7.下列命题中,正确的是( )
| A. | ?x0∈R,sinx0+cos0=$\frac{3}{2}$ | |
| B. | 已知X服从正态分布N(0,σ2),且p(-2<X≤2)=0.6,则P(X>2)=0.2 | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 命题“?x∈R,x2-x+1>0”的否定是“?x0∈R,x2-x+1<0” |
5.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+2≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$,则目标函数z=x+2y的最大值为( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | 0 | D. | 12 |
9.某产品的广告费用x万元与销售额y万元的统计数据如表:
根据上表可得回归方程$\widehaty=9.4x+a$,据此模型预测,广告费用为6万元时的销售额为( )万元.
| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 63.6 | B. | 65.5 | C. | 72 | D. | 67.7 |
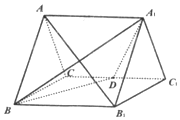 直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.