题目内容
13.在直角坐标系xOy中,曲线C1的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}sinα-cosα}\\{y=3-2\sqrt{3}sinαcosα-2co{s}^{2}α}\end{array}\right.$ (α为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.曲线C2的极坐标方程为ρsin(θ-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$m(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)若曲线C1与曲线C2有公共点,求实数m的取值范围.
分析 (1)利用三种方程的转化方法,求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)联立直线与抛物线,利用曲线C1与曲线C2有公共点,求实数m的取值范围.
解答 解:(1)曲线C1的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}sinα-cosα}\\{y=3-2\sqrt{3}sinαcosα-2co{s}^{2}α}\end{array}\right.$,消去参数,可得y=x2(-2≤x≤2)
曲线C2的极坐标方程为ρsin(θ-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$m,直角坐标方程为x-y+m=0;
(2)联立直线与抛物线可得x2-x-m=0,
∵曲线C1与曲线C2有公共点,
∴m=x2-x=(x-$\frac{1}{2}$)2-$\frac{1}{4}$,
∵-2≤x≤2,
∴-$\frac{1}{4}$≤m≤6.
点评 本题考查三种方程的转化,考查直线与抛物线位置关系的运用,属于中档题.

练习册系列答案
相关题目
1.已知函数f(x)=|lnx|,若f(m)=f(n)(m>n>0),则$\frac{2}{m+1}$+$\frac{2}{n+1}$=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
18.某人准备投资1200万元办一所中学,为了考虑社会效益和经济效益,对该地区教育市场进行调查,得出一组数据,列表如下(以班级为单位).
市场调查表:
根据物价部门的有关规定:初中是义务教育阶段,收费标准适当控制,预计除书本费、办公费外,初中每人每年可收取600元.高中每人每年可收取1500元.因生源和环境等条件限制,办学规模以20至30个班为宜(含20个班与30个),教师实行聘任制.初、高中教育周期均为三年,设初中编制为x个班,高中编制为y个班,请你合理地安排招生计划,使年利润最大.
市场调查表:
| 班级学生数 | 配备教师数 | 硬件建设费(万元) | 教师年薪(万元) | |
| 初中 | 50 | 2.0 | 28 | 1.2 |
| 高中 | 40 | 2.5 | 58 | 1.6 |
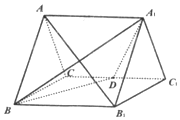 直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.