题目内容
若方程sinx=0的解集为E，方程sin2x=0的解集为F，则E，F的关系为（ ）
| A、E∩F=∅ | B、E=F |
| C、E?F | D、E⊆F |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：求出方程sinx=0的解集E，方程sin2x=0的解集F，即可得出结论．
解答：
解：方程sinx=0的解集为E={x|x=kπ，k∈Z}，方程sin2x=0的解集为F={x|x=
π，m∈Z}，
∴E⊆F．
故选：D．
| m |
| 2 |
∴E⊆F．
故选：D．
点评：本题考查集合的包含关系判断及应用，求出方程的解集是关键．
练习册系列答案
相关题目
已知函数f（x）=2sin（ωx+θ）（ω＞0，|θ|＜
）图象的对称中心与函数g（x）=tan（x+ϕ）图象的对称中心完全相同，且当x=
时，函数f（x）取得最大值，则函数f（x）的解析式是 ．
| π |
| 2 |
| π |
| 6 |
若S1=
exdx，S2=
2xdx，S3=
3xdx，则S1，S2，S3的大小关系为（ ）
| ∫ | 2 1 |
| ∫ | 2 1 |
| ∫ | 2 1 |
| A、S1＜S2＜S3 |
| B、S3＜S2＜S1 |
| C、S2＜S3＜S1 |
| D、S2＜S1＜S3 |
在复平面内，复数1+i对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在复平面内，复数z=
对应的点位于（ ）
| 1-i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合M={x|
＞0}，N={x|3x+2＞0}，则M∩N=（ ）
| x-3 |
| x+1 |
| A、（-∞，-1） | ||
B、（-1，-
| ||
C、（-
| ||
| D、（3，+∞） |
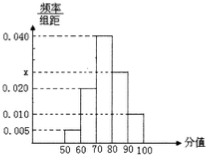为了全面推进素质教育，教育部门对某省500所中小学进行调研考评，考评分数在80分以上（含80分）的授予“素质教育先进学校”称号，考评统计结果如图的频率分布直方图所示，则应授予“素质教育先进学校”称号的学校有（ ）所．| A、125 | B、175 |
| C、325 | D、50 |
若命题“?（p∧q）”为真命题，则（ ）
| A、p、q均为真命题 |
| B、p、q中至少有一个为真命题 |
| C、p、q中至多有一个为真命题 |
| D、p、q均为假命题 |