题目内容
设F1、F2分别是椭圆E: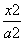 +
+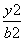 =1(a>b>0)的左、右焦点,M、N分别为其短轴的两个端点,且四边形MF1NF2的周长为4,设过F1的直线l与E相交于A、B两点,且|AB|=
=1(a>b>0)的左、右焦点,M、N分别为其短轴的两个端点,且四边形MF1NF2的周长为4,设过F1的直线l与E相交于A、B两点,且|AB|=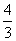 .
.
(1)求|AF2|·|BF2|的最大值;
(2)若直线l的倾斜角为45°,求△ABF2的面积.
解:(1)因为四边形MF1NF2为菱形,又其周长为4,故a=1
由椭圆定义知|AF2|+|AB|+|BF2|=4a=4,又因为|AB|=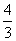 ,
,
所以|AF2|+|BF2|= ,
,
所以|AF2|·|BF2|≤ =
=
当且仅当|AF2|=|BF2|=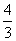 时,等号成立.
时,等号成立.
(此时AB⊥x轴,故可得A点坐标为 ,代入椭圆E的方程x2+
,代入椭圆E的方程x2+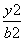 =1得b=
=1得b= <1,即当且仅当b=
<1,即当且仅当b= 时,|AF2|=|BF2|=
时,|AF2|=|BF2|=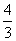 )
)
所以|AF2|·|BF2|的最大值为 .
.
(2)因为直线l的倾斜角为45°,所以可设l的方程为y=x+c,其中c= 

由(1)知椭圆E的方程为x2+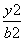 =1
=1
所以,设A(x1,y1),B(x2,y2),则A、B两点坐标满足方程组
化简得(1+b2)x2+2cx+1-2b2=0
则x1+x2= ,x1x2=
,x1x2=
因为直线l的斜率为1,所以|AB|= |x1-x2|
|x1-x2|
即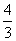 =
= |x1-x2|,所以
|x1-x2|,所以 =(x1+x2)2-4x1x2
=(x1+x2)2-4x1x2
 =
= ,得b2=
,得b2= ,b=
,b=
所以c= ,l的方程为:y=x+
,l的方程为:y=x+
F2到l的距离d=1.
所以S△ABC= |AB|×1=
|AB|×1= ×
×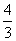 ×1=
×1= .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 |PN|.试建立平面直角坐标系,并求动点P的轨迹方程.
|PN|.试建立平面直角坐标系,并求动点P的轨迹方程.
 在椭圆C上,则椭圆C的标准方程为________.
在椭圆C上,则椭圆C的标准方程为________.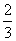 或
或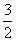 B.
B.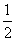 或2 D.
或2 D.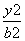 =1的左、右焦点,A是双曲线上在第一象限内的点,若|AF2|=2且∠F1AF2=45°.延长AF2交双曲线右支于点B,则△F1AB的面积等于________.
=1的左、右焦点,A是双曲线上在第一象限内的点,若|AF2|=2且∠F1AF2=45°.延长AF2交双曲线右支于点B,则△F1AB的面积等于________.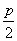 ;若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
;若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.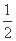 ,a4=4,则公比q= ;a1+a2+…+an= .
,a4=4,则公比q= ;a1+a2+…+an= .