题目内容
如右图所示，圆O1和圆O2的半径长都等于1，|O1O2|＝4.过动点P分别作圆O1，圆O2的切线PM，PN(M，N为切点)，使得|PM|＝
|PN|.试建立平面直角坐标系，并求动点P的轨迹方程．
解：以O1O2的中点O为原点，O1O2所在的直线为x轴，建立如图所示的平面直角坐标系，则O1(－2,0)，O2(2,0)．
由已知|PM|＝|PN|，
得|PM|2＝2|PN|2.
因为两圆的半径长均为1，所以|PO1|2－1＝2(|PO2|2－1)．
设P(x，y)，则(x＋2)2＋y2－1＝2[(x－2)2＋y2－1]，
化简，得(x－6)2＋y2＝33，所以所求轨迹方程为(x－6)2＋y2＝33.
[热点预测]
练习册系列答案
相关题目
x上时，求直线AB的方程．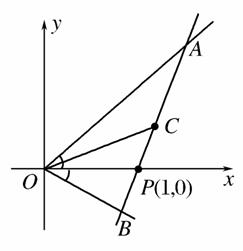
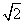时，求直线l的方程．
＋
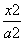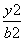＝1(a>b>0)的左、右焦点，M、N分别为其短轴的两个端点，且四边形MF1NF2的周长为4，设过F1的直线l与E相交于A、B两点，且|AB|＝
.
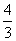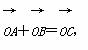，OC与AB交于点M.