题目内容
已知O为坐标原点，向量
=（sinα，1），
=（cosα，0），
=（-sinα，2），点P是直线AB上的一点，且
=
．
（Ⅰ）若O，P，C三点共线，求以线段OA，OB为邻边的平行四边形的对角线长；
（Ⅱ）记函数f（α）=
•
，α∈（-
，
），试求函数f（α）的值域．
| OA |
| OB |
| OC |
| AB |
| BP |
（Ⅰ）若O，P，C三点共线，求以线段OA，OB为邻边的平行四边形的对角线长；
（Ⅱ）记函数f（α）=
| BP |
| CA |
| π |
| 8 |
| π |
| 2 |
考点：平面向量数量积的运算,向量的模,平行向量与共线向量
专题：平面向量及应用
分析：（Ⅰ）设点P的坐标为（x，y），则由
=
求得x和y的值，可得点P的坐标．再根据
∥
求得cos2α=
，可得|
+
|=
和|
-
|的值，从而得出结论．
（Ⅱ）由条件化简f（α）为
sin(2α+
)，根据α∈(-
，
)，利用正弦函数的定义域和值域求得-1＜
sin(2α+
)≤
，可得f（α）的值域．
| AB |
| BP |
| OP |
| OC |
| 9 |
| 25 |
| OA |
| OB |
| (sinα+cosα)2+1 |
| OA |
| OB |
（Ⅱ）由条件化简f（α）为
| 2 |
| π |
| 4 |
| π |
| 8 |
| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
解答：
解：（Ⅰ）设点P的坐标为（x，y），则
=(cosα-sinα，-1)，
=(x-cosα，y)，
∵
=
，∴cosα-sinα=x-cosα，y=-1，∴x=2cosα-sinα，y=-1，
∴点P的坐标为（2cosα-sinα，-1）．
由O、P、C三点共线知：
∥
，（-1）×（-sinα）=2×（2cosα-sinα），
∴
=
，∵sin2α+cos2α=1∴cos2α=
，
∴|
+
|=
=
=
=
，
∴|
-
|=
=
=
=
，
∴以OA，OB为邻边的平行四边形的对角线长分别为
，
．
（Ⅱ）∵
=(cosα-sinα，-1)，
=(2sinα，-1)，
∴f（α）=2sinα（cosα-sinα）+1=sin2α+cos2α=
sin(2α+
)．
∵α∈(-
，
)，∴0＜2α+
＜
，
∴-
＜sin(2α+
)≤1，-1＜
sin(2α+
)≤
．
∴f（α）的值域为(-1，
]．
| AB |
| BP |
∵
| AB |
| BP |
∴点P的坐标为（2cosα-sinα，-1）．
由O、P、C三点共线知：
| OP |
| OC |
∴
| sinα |
| cosα |
| 4 |
| 3 |
| 9 |
| 25 |
∴|
| OA |
| OB |
| (sinα+cosα)2+1 |
| 2sinαcosα+2 |
|
| ||
| 5 |
∴|
| OA |
| OB |
| (sinα-cosα)2+1 |
| 2-2sinαcosα |
2-
|
| ||
| 5 |
∴以OA，OB为邻边的平行四边形的对角线长分别为
| ||
| 5 |
| ||
| 5 |
（Ⅱ）∵
| BP |
| CA |
∴f（α）=2sinα（cosα-sinα）+1=sin2α+cos2α=
| 2 |
| π |
| 4 |
∵α∈(-
| π |
| 8 |
| π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
∴-
| ||
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
∴f（α）的值域为(-1，
| 2 |
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，求向量的模的方法，三角恒等变换，正弦函数的定义域和值域，属于中档题．
练习册系列答案
相关题目
设集合A={a，b}，集合B={5，log2（a+3）}，若A∩B={2}，则A∪B等于（ ）
| A、{2，5，7} |
| B、{-1，2，5} |
| C、{1，2，5} |
| D、{-7，2，5} |
某班有12名男生和18名女生参加综合素质测试，所得分数的茎叶图如图，若成绩在75分以上（包括75分）定义为“优秀”，成绩在75分以下（不包括75分）定义为“非优秀”．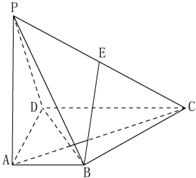
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．