题目内容
1．大学生村官王善良落实政府“精准扶贫”，帮助贫困户张三用9万元购进一部节能环保汽车，用于出租，假设第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加2万元，该车每年的运营收入均为11万元，若该车使用了n（n∈N*）年后，年平均盈利额达到最大值（盈利额等于收入减去成本），则n等于3．分析 根据题意建立等差数列模型，利用等差数列的性质以及求和公式即可得到结论．
解答 解：设该汽车第n年的营运费为an，万元，则数列{an}是以2为首项，2为公差的等差数列，则an=2n，
则该汽车使用了n年的营运费用总和为Tn=n2+n，
设第n年的盈利总额为Sn，则Sn=11n-（n2+n）-9=-n2+10n-9，
∴年平均盈利额P=10-（n+$\frac{9}{n}$）
当n=3时，年平均盈利额取得最大值4，
故答案为：3．
点评 本题主要考查与数列有关的应用问题，根据条件利用等差数列的通项公式求出盈利总额的表达式是解决本题的关键．
练习册系列答案
相关题目
在如图所示的五面体中，四边形ABCD是矩形，平面ADF⊥平面ABEF，且AB∥EF，AB=$\frac{1}{2}$EF=2$\sqrt{2}$，AF=BE=2，M是EF的中点，N在AM上．
13．已知函数f（x）=$\left\{\begin{array}{l}{sinx+2cos2x，x≥0}\\{-{e}^{2x}，x＜0}\\{\;}\end{array}\right.$，则f（f（$\frac{π}{2}$））等于（ ）
| A． | -$\frac{1}{{e}^{2}}$ | B． | $\frac{1}{{e}^{2}}$ | C． | -e2 | D． | e2 |
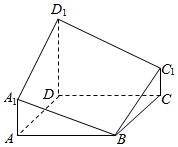如图所示的多面体是经过正四棱柱底面顶点B作截面A1BC1D1后形成的．已知AB=1，A1A=C1C=$\frac{1}{2}{D_1}$D，D1B与底面ABCD所成的角为$\frac{π}{3}$，则这个多面体的体积为$\frac{\sqrt{6}}{2}$．