题目内容
3.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1,F2.若左焦点F1关于其中一条渐近线的对称点位于双曲线上,则该双曲线的离心率e的值为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
分析 设左焦点F1(-c,0),渐近线方程为y=$\frac{b}{a}$x,对称点为F'(m,n),运用中点坐标公式和两直线垂直的条件:斜率之积为-1,求出对称点的坐标,代入双曲线的方程,由离心率公式计算即可得到所求值.
解答 解:设F1(-c,0),渐近线方程为y=$\frac{b}{a}$x,
对称点为F'(m,n),
即有$\frac{n}{m+c}$=-$\frac{a}{b}$,
且$\frac{1}{2}$•n=$\frac{1}{2}$•$\frac{b(m-c)}{a}$,
解得m=$\frac{{b}^{2}-{a}^{2}}{c}$,n=-$\frac{2ab}{c}$,
将F'($\frac{{b}^{2}-{a}^{2}}{c}$,-$\frac{2ab}{c}$),即($\frac{{c}^{2}-2{a}^{2}}{c}$,-$\frac{2ab}{c}$),
代入双曲线的方程可得$\frac{({c}^{2}-2{a}^{2})^{2}}{{c}^{2}{a}^{2}}$-$\frac{4{a}^{2}{b}^{2}}{{c}^{2}{b}^{2}}$=1,
化简可得$\frac{{c}^{2}}{{a}^{2}}$-4=1,即有e2=5,
解得e=$\sqrt{5}$.
故选:C.
点评 本题考查双曲线的离心率的求法,注意运用中点坐标公式和两直线垂直的条件:斜率之积为-1,以及点满足双曲线的方程,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
13.经过点(3,-$\sqrt{2}$)的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,其一条渐近线方程为y=$\frac{\sqrt{3}}{3}$x,该双曲线的焦距为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
18.经过点(2,1),且渐近线与圆x2+(y-2)2=1相切的双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{\frac{11}{3}}$-$\frac{{y}^{2}}{11}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | $\frac{{y}^{2}}{\frac{11}{3}}$-$\frac{{x}^{2}}{11}$=1 | D. | $\frac{{y}^{2}}{11}$-$\frac{{x}^{2}}{\frac{11}{3}}$=1 |
13.3位同学各自参加甲、乙两个兴趣小组,则两个兴趣小组都有同学参加的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{9}$ | D. | $\frac{3}{4}$ |
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.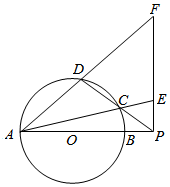 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
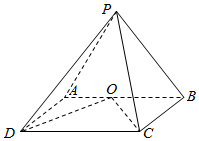 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.