题目内容
2loga(M-2N)=logaM+logaN,则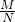 的值为________.
的值为________.
4
分析:利用对数的运算法则将已知等式转化为(M-2N)2=MN,两边同时除以N2得到方程 ,解方程求出
,解方程求出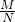 的值,注意M,N的范围.
的值,注意M,N的范围.
解答:因为2loga(M-2N)=logaM+logaN,
所以loga(M-2N)2=loga(MN),
所以(M-2N)2=MN,
所以M2-4MN+4N2=MN,
所以 ,
,
所以 或1,
或1,
因为M>2N
所以 ,
,
故答案为:4
点评:本题考查对数的运算法则及对数的真数必须大于0,属于基础题.
分析:利用对数的运算法则将已知等式转化为(M-2N)2=MN,两边同时除以N2得到方程
 ,解方程求出
,解方程求出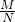 的值,注意M,N的范围.
的值,注意M,N的范围.解答:因为2loga(M-2N)=logaM+logaN,
所以loga(M-2N)2=loga(MN),
所以(M-2N)2=MN,
所以M2-4MN+4N2=MN,
所以
 ,
,所以
 或1,
或1,因为M>2N
所以
 ,
,故答案为:4
点评:本题考查对数的运算法则及对数的真数必须大于0,属于基础题.

练习册系列答案
相关题目
2loga(M-2N)=logaM+logaN,则
的值为( )
| M |
| N |
A、
| ||
| B、4 | ||
| C、1 | ||
| D、4或1 |
 的值为( )
的值为( )