题目内容
已知函数f(x)=
-
(a为常数)
(1)若y=f(x)为奇函数,求出a的值;
(2)在满足(1)的条件下,探索y=f(x)的单调性,并利用定义加以证明.
| a |
| 2 |
| 2x |
| 2x+1 |
(1)若y=f(x)为奇函数,求出a的值;
(2)在满足(1)的条件下,探索y=f(x)的单调性,并利用定义加以证明.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据奇函数的性质,利用f(0)=0,即可得到结论.
解答:
解:(1)函数f(x)的定义域R,
∵f(x)是R上的奇函数,
∴f(0)=0,
即f(0)=
-
=
=0,
解得a=1;
经验证a=1时函数f(x)为R上的奇函数.
(2)若f(x)为R上的奇函数,则a=1,即f(x)=
-
,
设x1<x2,
则f(x1)-f(x2)=
-
-
+
=
,
∵y=2x是R上的增函数,
2x2-2x1>0,
∴即f(x1)-f(x2)>0
f(x1)>f(x2),
∴函数y=f(x)在R上是减函数.
∵f(x)是R上的奇函数,
∴f(0)=0,
即f(0)=
| a |
| 2 |
| 1 |
| 1+1 |
| a-1 |
| 2 |
解得a=1;
经验证a=1时函数f(x)为R上的奇函数.
(2)若f(x)为R上的奇函数,则a=1,即f(x)=
| 1 |
| 2 |
| 2x |
| 2x+1 |
设x1<x2,
则f(x1)-f(x2)=
| 1 |
| 2 |
| 2x1 |
| 2x1+1 |
| 1 |
| 2 |
| 2x2 |
| 2x2+2 |
| 2x2-2x1 |
| (2x1+1)(2x2+1) |
∵y=2x是R上的增函数,
2x2-2x1>0,
∴即f(x1)-f(x2)>0
f(x1)>f(x2),
∴函数y=f(x)在R上是减函数.
点评:本题主要考查函数单调性的判断和证明以及函数奇偶性的应用,利用定义法以及奇函数f(0)=0的性质是解决本题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知点P是边长为1的正三角形内一点,该点到三角形三边的距离分别是a,b,c(a,b,c>0),则ab+bc+ca的取值范围是( )
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、[
|
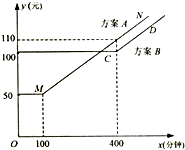 移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).
移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).