题目内容
3．
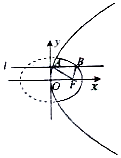如图动直线l：y=b与抛物线y2=4x交于点A，与椭圆$\frac{x^2}{2}+{y^2}$=1交于抛物线右侧的点B，F为抛物线的焦点，则|AF|+|BF|+|AB|的最大值为（ ）| A． | $3\sqrt{3}$ | B． | $3\sqrt{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
分析 利用抛物线的定义，求出抛物线的焦点坐标，求出B的坐标，转化所求的距离为x的函数的关系式，然后求解最大值即可．
解答 
解：直线l：y=b与抛物线y2=4x交于点A，F为抛物线的焦点，直线y=b与x=-1的交点为D，由抛物线定义，可知AF=AD，|AF|+|BF|+|AB|的最大值，
就是BD+BF的最大值，F（1，0），设B（x，b），椭圆$\frac{x^2}{2}+{y^2}$=1的焦点坐标（1，0）．
可得$\frac{{x}^{2}}{2}+{b}^{2}=1$，|AF|+|BF|+|AB|=x+1+$\sqrt{（x-1）^{2}+{b}^{2}}$=x+1+$\sqrt{（x-1）^{2}+1-\frac{{x}^{2}}{2}}$
=x+1+$\sqrt{\frac{{x}^{2}}{2}-2x+2}$=x+1+$\frac{\sqrt{2}}{2}（2-x）$=1+$\sqrt{2}$+x（1-$\frac{\sqrt{2}}{2}$），x∈（0，$\sqrt{2}$]．
当x=$\sqrt{2}$时，1+$\sqrt{2}$+x（1-$\frac{\sqrt{2}}{2}$）=1+$\sqrt{2}$+$\sqrt{2}$（1-$\frac{\sqrt{2}}{2}$）=2$\sqrt{2}$，
故选：D．
点评 本题考查直线与椭圆以及抛物线的位置关系的综合应用，考查函数思想的应用，是中档题．
练习册系列答案
相关题目
11．设F1，F2分别为椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1（{a_1}＞{b_1}＞0）$与双曲线C2：$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1（{a_2}＞0，{b_2}＞0）$的公共焦点，它们在第一象限内交于点M，∠F1MF2=90°，若椭圆的离心率${e_1}=\frac{3}{4}$，则双曲线C2的离心率e2的值为（ ）
| A． | $\frac{9}{2}$ | B． | $\frac{{3\sqrt{2}}}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{5}{4}$ |
18．在如图所示的程序图中，若函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，αx≤0}\\{lo{g}_{\frac{1}{2}}x，x＞0}\end{array}\right.$，则输出的结果是（ ）
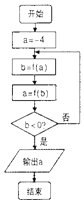
| A． | -3 | B． | $\frac{1}{16}$ | C． | $\frac{1}{4}$ | D． | 4 |
8．某个路口交通指示灯，红灯时间为30秒，黄灯时间为10秒，绿灯时间为40秒，黄灯时间可以通行，当你到达路口时，等待时间不超过10秒就可以通行的概率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{7}$ | C． | $\frac{5}{7}$ | D． | $\frac{5}{8}$ |
3．过点M（0，1）和N（-1，m2）（m∈R）的直线的倾斜角α的取值范围是（ ）
| A． | 0°≤α＜180° | B． | 45°≤α＜180° | ||
| C． | 0°≤α≤45°或90°＜α＜180° | D． | 0°≤α≤45°或90°≤α＜180° |