题目内容
【题目】已知![]() ,直线
,直线![]() 经过定点
经过定点![]() ,直线
,直线![]() 经过定点
经过定点![]() ,且
,且![]() 与
与![]() 相交于
相交于![]() 点,这两条直线与两坐标轴围成的四边形面积为
点,这两条直线与两坐标轴围成的四边形面积为![]() .
.
(1)证明:![]() ,并求定点
,并求定点![]() 、
、![]() 的坐标;
的坐标;
(2)求三角形![]() 面积最大值,以及
面积最大值,以及![]() 时的
时的![]() .
.
【答案】(1)证明见解析,![]() ,
,![]() ;(2)三角形
;(2)三角形![]() 面积最大值为
面积最大值为![]() ,
,![]() .
.
【解析】
(1)先由![]() 得到
得到![]() ,即可求出
,即可求出![]() ;再由
;再由![]() 得到
得到![]() ,即可求出
,即可求出![]() ;根据两直线的斜率之积,即可判断直线垂直;
;根据两直线的斜率之积,即可判断直线垂直;
(2)先分别记点![]() 到直线
到直线![]() 的距离为
的距离为![]() 、点
、点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,由点到直线距离公式求出
,由点到直线距离公式求出![]() ,
,![]() ,表示出
,表示出 ,根据基本不等式求出最值,再由
,根据基本不等式求出最值,再由![]() ,结合极限的运算,即可得出结果.
,结合极限的运算,即可得出结果.
(1)因为![]() 可化为
可化为![]() ,因此易知
,因此易知![]() 过点
过点![]() ,即
,即![]() ;
;
由![]() 可得:
可得:![]() ,因此直线
,因此直线![]() 过点
过点![]() ;
;
又![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ;直线
;直线![]() 的斜率为
的斜率为![]() ;所以
;所以![]() ,因此
,因此![]() ;
;
(2)分别记点![]() 到直线
到直线![]() 的距离为
的距离为![]() 、点
、点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则![]() ,
,![]() ,
,
由(1)可得:![]() ,
,
所以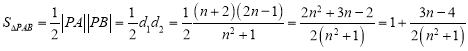 ,
,
令![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,则
时,则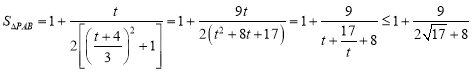 ,
,
当且仅当![]() ,即
,即![]() ,即
,即![]() 时,等号成立,
时,等号成立,
又![]() ,
,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
综上三角形![]() 面积最大值为
面积最大值为![]() ;
;
又两条直线与两坐标轴围成的四边形面积为
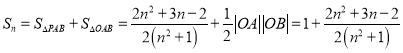 ;
;
所以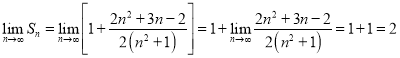 .
.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】世界卫生组织的最新研究报告显示,目前中国近视患者人数多达6亿,高中生和大学生的近视率均已超过七成,为了研究每周累计户外暴露时间(单位:小时)与近视发病率的关系,对某中学一年级200名学生进行不记名问卷调查,得到如下数据:
每周累积户外暴露时间(单位:小时) |
|
|
|
| 不少于28小时 |
近视人数 | 21 | 39 | 37 | 2 | 1 |
不近视人数 | 3 | 37 | 52 | 5 | 3 |
(1)在每周累计户外暴露时间不少于28小时的4名学生中,随机抽取2名,求其中恰有一名学生不近视的概率;
(2)若每周累计户外暴露时间少于14个小时被认证为“不足够的户外暴露时间”,根据以上数据完成如下列联表,并根据(2)中的列联表判断能否在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系?
近视 | 不近视 | |
足够的户外暴露时间 | ||
不足够的户外暴露时间 |
附:![]()
P | 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |