题目内容
【题目】已知椭圆![]() :
:![]() 的左右焦点分别是
的左右焦点分别是![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 有相同的焦点,点
有相同的焦点,点![]() 为抛物线与椭圆
为抛物线与椭圆![]() 在第一象限的交点,且满足
在第一象限的交点,且满足![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,设
两点,设![]() .若
.若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意可得点P的坐标为![]() ,然后求出
,然后求出![]() ,根据椭圆的定义可得
,根据椭圆的定义可得![]() ,进而得到
,进而得到![]() ,于是可得椭圆的方程.(2)由题意直线
,于是可得椭圆的方程.(2)由题意直线![]() 的斜率不为0,设其方程为
的斜率不为0,设其方程为![]() ,代入椭圆方程后结合根与系数的关系得到
,代入椭圆方程后结合根与系数的关系得到![]() ,然后通过换元法求出
,然后通过换元法求出![]() 的范围即可.
的范围即可.
(1)由题意得抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,准线方程为
,准线方程为![]() .
.
∵![]() ,
,
∴点P到直线![]() 的距离为
的距离为![]() ,从而点P的横坐标为
,从而点P的横坐标为![]() ,
,
又点P在第一象限内,
∴点P的坐标为![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)根据题意得直线![]() 的斜率不为0,设其方程为
的斜率不为0,设其方程为![]() ,
,
由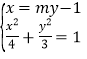 消去
消去![]() 整理得
整理得![]() ,
,
显然![]() .
.
设![]() ,则
,则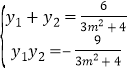 ①
①
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
代入①消去![]() 得
得![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() .
.
由题意得![]() .
.
令![]() ,则
,则![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
即![]() 面积的取值范围为
面积的取值范围为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了对某课题进行研究,用分层抽样方法从三所高校![]() ,
,![]() ,
,![]() 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
高校 | 相关人员 | 抽取人数 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(1)求![]() ,
,![]() ;
;
(2)若从高校![]() ,
,![]() 抽取的人中选2人做专题发言,求这2人都来自高校
抽取的人中选2人做专题发言,求这2人都来自高校![]() 的概率.
的概率.