题目内容
【题目】设命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() ;命题
;命题![]() :关于
:关于![]() 的方程
的方程![]() 有实根.
有实根.
(1)如果![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围.
的取值范围.
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 实数![]() 的取值范围为
的取值范围为![]() ;(2) 实数
;(2) 实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
【解析】试题分析:(1)由函数![]() 的定义域为
的定义域为![]() 可得
可得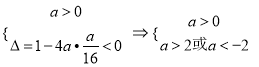 ,可得实数
,可得实数![]() 的取值范围为
的取值范围为![]() ;(2)化简命题
;(2)化简命题![]() 可得
可得![]() ,由
,由![]() 为真命题,
为真命题, ![]() 为假命题,可得
为假命题,可得![]() 一真一假,分两种情况讨论,对于
一真一假,分两种情况讨论,对于![]() 真
真![]() 假以及
假以及![]() 假
假![]() 真分别列不等式组,分别解不等式组,然后求并集即可求得实数
真分别列不等式组,分别解不等式组,然后求并集即可求得实数![]() 的取值范围.
的取值范围.
试题解析:(1)若命题![]() 是真命题,则有①当
是真命题,则有①当![]() 时定义域为
时定义域为![]() ,不合题意
,不合题意
②当![]() 时,由已知可得
时,由已知可得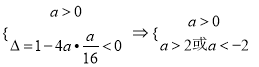
故所求实数![]() 的取值范围为
的取值范围为![]()
(2)若命题![]() 是真命题,则关于
是真命题,则关于![]() 的方程
的方程![]() 有实根,令
有实根,令![]() ,
,
![]() ∴
∴![]()
若命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,则
”为假命题,则![]() 一真一假
一真一假
若![]() 真
真![]() 假,则
假,则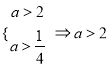 ;若
;若![]() 假
假![]() 真,则
真,则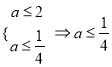
综上:实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

练习册系列答案
相关题目