题目内容
20.设实数x,y满足$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=x+3y的最小值为( )| A. | -6 | B. | -3 | C. | 5 | D. | 27 |
分析 画出满足约束条件表示的平可行域,然后分析平面区域里各个角点,然后将其代入z=x+3y中,求出最小值即可.
解答 解:满足约束条件的可行域如下图示: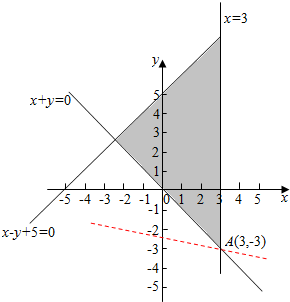
z=x+3y的最小值就是直线在y轴上的截距的$\frac{1}{3}$倍,
由$\left\{\begin{array}{l}{x=3}\\{x+y=0}\end{array}\right.$,解得A(3,-3),
由图可知,z=x+3y经过的交点A(3,-3)时,
Z=x+3y有最小值-6,
故选:A.
点评 在解决线性规划的小题时,常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
相关题目
10.不等式ax2+5x-2>0的解集是{x|$\frac{1}{2}$<x<2},则关于x的不等式ax2-5x+a2-1>0的解集为( )
| A. | (-∞,-$\frac{3}{2}$)∪(1,+∞) | B. | (-$\frac{3}{2}$,1) | C. | (-∞-3)∪($\frac{1}{2}$,+∞) | D. | (-3,$\frac{1}{2}$) |
8.若cosα+sinα=$\frac{2}{3}$,则$\frac{\sqrt{2}sin(2α-\frac{π}{4})+1}{1+tanα}$的值为( )
| A. | $\frac{5}{9}$ | B. | 0 | C. | -$\frac{5}{18}$ | D. | -$\frac{5}{9}$ |
15.给出函数f(x)=a2x-1+2(a为常数,且a>0,a≠1),无论a取何值,函数f(x)恒过定点P,则P的坐标是( )
| A. | (0,1) | B. | (1,2) | C. | (1,3) | D. | ($\frac{1}{2}$,3) |
12.对甲、乙两个班级的某次数学成绩进行统计,按照大于等于85分为优秀,85分以下为非优秀,得到如下所示的列联表:
已知在全部的105人中随机抽取1人,成绩优秀的概率为$\frac{2}{7}$.
(1)求b,c的值;
(2)根据表闻表中的数据,运用独立检验的思想方法分析:学生的数学成绩与班级是否有关系?并说明理由.
附:参考公式与临界值表:K2=$\frac{n(ab-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | b | |
| 乙班 | c | 30 | |
| 总计 | 105 |
(1)求b,c的值;
(2)根据表闻表中的数据,运用独立检验的思想方法分析:学生的数学成绩与班级是否有关系?并说明理由.
附:参考公式与临界值表:K2=$\frac{n(ab-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥K0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |