题目内容
已知直线l的参数方程: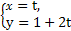 (t为参数)和圆C的极坐标方程:ρ=2
(t为参数)和圆C的极坐标方程:ρ=2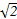 sin(θ+
sin(θ+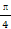 ),判断直线和圆C的位置关系.
),判断直线和圆C的位置关系.
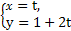 (t为参数)和圆C的极坐标方程:ρ=2
(t为参数)和圆C的极坐标方程:ρ=2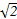 sin(θ+
sin(θ+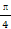 ),判断直线和圆C的位置关系.
),判断直线和圆C的位置关系.相交,理由见解析
直线l的普通方程为y=2x+1,
圆C:ρ=2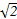 sin(θ+
sin(θ+ )即ρ=2(sinθ+cosθ),
)即ρ=2(sinθ+cosθ),
∴ρ2=2ρsinθ+2ρcosθ,
∴x2+y2=2x+2y.
即(x-1)2+(y-1)2=2.
∵圆心到直线的距离为d= =
= <
<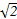 ,
,
∴直线l与圆C相交.
圆C:ρ=2
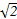 sin(θ+
sin(θ+ )即ρ=2(sinθ+cosθ),
)即ρ=2(sinθ+cosθ),∴ρ2=2ρsinθ+2ρcosθ,
∴x2+y2=2x+2y.
即(x-1)2+(y-1)2=2.
∵圆心到直线的距离为d=
 =
= <
<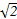 ,
,∴直线l与圆C相交.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
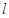 :
: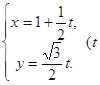 为参数), 曲线
为参数), 曲线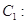
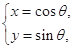 (
(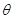 为参数).
为参数).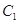 相交于
相交于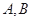 两点,求
两点,求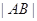 ;
;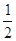 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的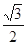 倍,得到曲线
倍,得到曲线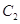 ,设点
,设点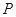 是曲线
是曲线 曲线C2的参数方程为
曲线C2的参数方程为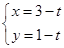 (
(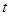 为参数),以极点为原点,极轴为
为参数),以极点为原点,极轴为 轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为
轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为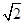
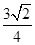
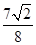
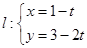 (
(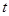 为参数且
为参数且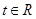 )与曲线
)与曲线 (
(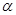 是参数且
是参数且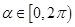 ),则直线
),则直线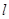 与曲线
与曲线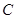 的交点坐标为.
的交点坐标为.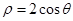 在点
在点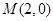 处的切线的极坐标方程为 .
处的切线的极坐标方程为 .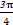 )=
)=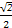 ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0,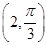 ,半径R=
,半径R=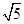 ,求圆C的极坐标方程.
,求圆C的极坐标方程. 与曲线
与曲线 (
( 为参数)无公共点,则过点
为参数)无公共点,则过点 的直线与曲线
的直线与曲线 的公共点的个数为 .
的公共点的个数为 .