题目内容
4.坛子里放着5个相同大小,相同形状的咸鸭蛋,其中有3个是绿皮的,2个是白皮的.如果不放回地依次拿出2个鸭蛋,求:(1)第一次拿出绿皮鸭蛋的概率;
(2)第1次和第2次都拿到绿皮鸭蛋的概率;
(3)在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率.
分析 (1)从5个鸭蛋中不放回地依次拿出2个的基本事件数为μ(Ω)=A52=20.又μ(A)=A31×A41=12,可得第一次拿出绿皮鸭蛋的概率;
(2)因为μ(AB)=A32=6,利用P(AB)=$\frac{μ(AB)}{μ(Ω)}$,求出第1次和第2次都拿到绿皮鸭蛋的概率;
(3)利用条件概率,求出在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率.
解答 解:设第1次拿出绿皮鸭蛋为事件A,第2次拿出绿皮鸭蛋为事件B,则第1次和第2次都拿出绿皮鸭蛋为事件AB.
(1)从5个鸭蛋中不放回地依次拿出2个的基本事件数为μ(Ω)=A52=20.
又μ(A)=A31×A41=12.于是P(A)=$\frac{μ(A)}{μ(Ω)}$=$\frac{12}{20}$=$\frac{3}{5}$.
(2)因为μ(AB)=A32=6,所以P(AB)=$\frac{μ(AB)}{μ(Ω)}$=$\frac{6}{20}$=$\frac{3}{10}$.
(3)因为μ(AB)=6,μ(A)=12,所以P(B|A)=$\frac{μ(AB)}{μ(A)}$=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查概率的计算,考查条件概率,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
19. 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )
 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )| A. | (1)和(3) | B. | (2)和(5) | C. | (1)和(4) | D. | (2)和(4) |
16.若正数a,b满足ab-(a+b)=1,则a+b的最小值是( )
| A. | 2+2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
 ,
,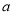 是
是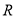 上的常数,若
上的常数,若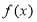 的值域为
的值域为 ,则
,则 取值范围为( )
取值范围为( )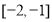 B.
B.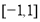
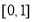 D.
D.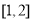
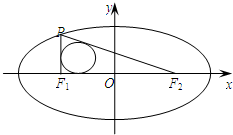 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0.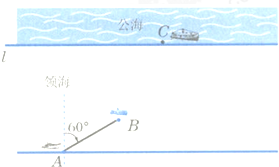 设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:
设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题: