题目内容
16.若正数a,b满足ab-(a+b)=1,则a+b的最小值是( )| A. | 2+2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
分析 由已知结合基本不等式可得$\frac{(a+b)^{2}}{4}$-(a+b)≥1,解得a+b的范围,进而可得a+b的最小值.
解答 解:∵正数a,b满足$\frac{a+b}{2}$$≥\sqrt{ab}$,
故ab≤$\frac{(a+b)^{2}}{4}$,
若ab-(a+b)=1,则$\frac{(a+b)^{2}}{4}$-(a+b)≥1,
解得:a+b≥2+2$\sqrt{2}$,
即a+b的最小值是2+2$\sqrt{2}$,
故选:A.
点评 本题考查的知识点是基本不等式在最值问题中的应用,熟练掌握基本不等式的适用范围,是解答的关键.

练习册系列答案
相关题目
6.在三棱锥P-ABC中,PA⊥底面ABC,BC⊥AC,∠ABC=30°,AC=1,PB=2$\sqrt{3}$,则PC与平面PAB所成余弦值是( )
| A. | $\frac{\sqrt{33}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
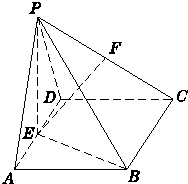 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.