题目内容
14.椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点P(x0,y0),其中${x}_{0}^{2}$=$\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}-{b}^{2}}$,求离心率的范围.分析 由椭圆上点P的横坐标的值,得到关于a,b,c的不等式,求出e的范围,再与0<e<1取交集得答案.
解答 解:∵P(x0,y0)是椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点,
∴0≤${x}_{0}^{2}$=$\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}-{b}^{2}}$≤a2,
即$\left\{\begin{array}{l}{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}≥0}\\{\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}-{b}^{2}}≤{a}^{2}}\end{array}\right.$,解得:$e≥\frac{\sqrt{2}}{2}$.
又0<e<1,
∴$\frac{\sqrt{2}}{2}≤e<1$.
点评 本题考查椭圆的简单性质,关键是把椭圆上点的横坐标转化为含有a,b,c的不等式,是基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体的体积为( )
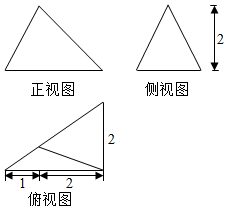

| A. | $\frac{4}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 3 | D. | 2 |
3.在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x,其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)都有不等式$t<\frac{{{{({e_1}+{e_2})}^2}}}{8}$恒成立,则t的最大值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{4}$ |
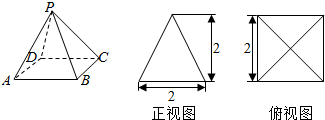 四棱锥P-ABCD及其正(主)视图和俯视图如图所示.
四棱锥P-ABCD及其正(主)视图和俯视图如图所示.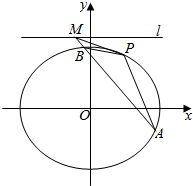 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.