题目内容
2.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F.短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点.若|AF|+|BF|=4,点M到直线l的距离不小于$\frac{4}{5}$,则椭圆E的离心率的取值范围是$({0,\frac{{\sqrt{3}}}{2}}]$.分析 如图所示,设F′为椭圆的左焦点,连接AF′,BF′,则四边形AFBF′是平行四边形,可得4=|AF|+|BF|=|AF′|+|BF|=2a.取M(0,b),由点M到直线l的距离不小于$\frac{4}{5}$,得到关于b的不等式,求出b的范围.再利用离心率计算公式e=$\frac{c}{a}$即可得出.
解答 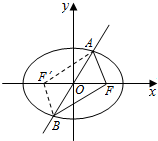 解:如图所示,
解:如图所示,
设F′为椭圆的左焦点,连接AF′,BF′,则四边形AFBF′是平行四边形,
∴4=|AF|+|BF|=|AF′|+|AF|=2a,∴a=2.
取M(0,b),∵点M到直线l的距离不小于$\frac{4}{5}$,
∴$\frac{|4b|}{\sqrt{{3}^{2}{+4}^{2}}}$≥$\frac{4}{5}$,解得b≥1.
∴e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$≤$\sqrt{1-\frac{1}{{2}^{2}}}$=$\frac{\sqrt{3}}{2}$.
∴椭圆E的离心率的取值范围是(0,$\frac{\sqrt{3}}{2}$].
故答案为:$({0,\frac{{\sqrt{3}}}{2}}]$.
点评 本题考查了椭圆的定义标准方程及其性质、点到直线的距离公式、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.(1-x)9的展开式按x的升幂排列,系数最大的项是第( )项.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
3.三种细菌A,B,C分别按照一定的比率繁殖,A在两天中繁殖为原来的2倍,B在三天中繁殖为原来的3倍,C在四天中繁殖为原来的4倍,设A,B,C三种细菌每天的繁殖速度分别记为a,b,c,则( )
| A. | a>b>c | B. | b>a>c | C. | c=a>b | D. | b>a=c |