题目内容
19.某几何体的三视图如图所示,则该几何体的体积为( )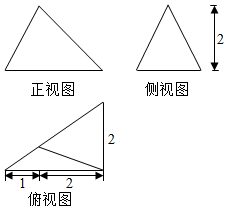
| A. | $\frac{4}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 3 | D. | 2 |
分析 根据三视图判断几何体为三棱锥,且三棱锥的一个侧面垂直于底面,高为2,三棱锥的底面为直角三角形,矩直角边长分别为3、2,把数据代入棱锥的体积公式计算.
解答 解:由题意,几何体为三棱锥,且三棱锥的一个侧面垂直于底面,高为2,
三棱锥的底面为直角三角形,矩直角边长分别为3、2,
∴几何体的体积V=$\frac{1}{3}$×$\frac{1}{2}$×3×2×2=2.
故选:D.
点评 本题考查了由三视图求几何体的体积,解题的关键是由三视图判断几何体的形状及判断数据所对应的几何量.

练习册系列答案
相关题目
3.三种细菌A,B,C分别按照一定的比率繁殖,A在两天中繁殖为原来的2倍,B在三天中繁殖为原来的3倍,C在四天中繁殖为原来的4倍,设A,B,C三种细菌每天的繁殖速度分别记为a,b,c,则( )
| A. | a>b>c | B. | b>a>c | C. | c=a>b | D. | b>a=c |
4.几何体的三视图如图所示,则该几何体的体积为( )
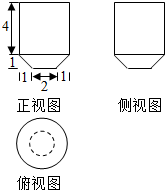

| A. | $\frac{53}{3}$π | B. | $\frac{55}{3}$π | C. | 18π | D. | $\frac{76}{3}$π |
8.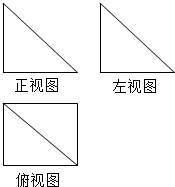 一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )
一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )
 一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )
一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )| A. | 32$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 48π | D. | 12π |
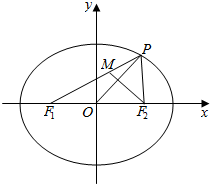 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.