题目内容
命题：任意x∈R，使x2+x+7＞0的否定为 ．
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题是否定是特称命题写出结果即可．
解答：
解：因为全称命题的否定是特称命题，所以，命题任意x∈R，使x2+x+7＞0的否定是：存在x0∈R，x02+x0+7≤0．
故答案为：存在x0∈R，x02+x0+7≤0．
故答案为：存在x0∈R，x02+x0+7≤0．
点评：本题考查命题的否定特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
已知幂函数y=f（x）的图象经过点（2，4），则f（3）=（ ）
| A、3 | ||
B、
| ||
| C、9 | ||
D、
|
阅读如图所示的程序框图，运行相应的程序，若输出的结果是24，则判断框中应填入的内容为（ ）
| A、n≤3？ | B、n≤4？ |
| C、n≤5？ | D、n≤6？ |
复数-
的共轭复数是（ ）
| 1+i |
| i |
| A、1-i | B、-1+i |
| C、1+i | D、-1-i |
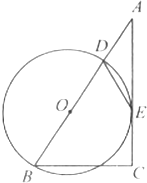如图，在Rt△ABC中，∠A=30°，∠C=90°，D是AB边上的一点，以BD为直径的⊙O与AC相切于点E．若BC=6，则DE的长为过抛物线y2=4x（p＞0）的焦点作两条互相垂直的弦AB、CD，则
+
=（ ）
| 1 |
| |AB| |
| 1 |
| |CD| |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|