题目内容
抛掷三枚不同的具有正、反两面的金属制品 ,假定
,假定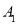 正面向上的概率为
正面向上的概率为 ,
,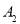 正面向上的概率为
正面向上的概率为 ,
, 正面向上的概率为t(0<t<1),把这三枚金属制品各抛掷一次,设
正面向上的概率为t(0<t<1),把这三枚金属制品各抛掷一次,设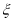 表示正面向上的枚数。
表示正面向上的枚数。
(1)求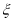 的分布列及数学期望
的分布列及数学期望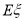 (用t表示);
(用t表示);
(2)令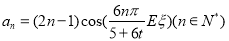 ,求数列
,求数列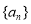 的前n项和.
的前n项和.
(I) ;(II)
;(II)
【解析】
试题分析:(I) 的所以可能取值为1,2,3,
的所以可能取值为1,2,3, ,
,

 ,
, ,从而可得到分布列和期望;(II)
,从而可得到分布列和期望;(II) ,需分n的奇偶性来讨论
,需分n的奇偶性来讨论
试题解析:(I) 的所以可能取值为1,2,3
的所以可能取值为1,2,3





所以 的分布列为
的分布列为



(II)
当n为偶数时,
当n为奇数时,
综上
考点:概率与统计

练习册系列答案
相关题目
 的单调函数
的单调函数 ,若对任意的
,若对任意的 ,都有
,都有 ,则方程
,则方程 的解的个数是
的解的个数是 ,B=
,B= ,则
,则
 B.
B.
 D.
D. 
 ,
, 和平面
和平面 ,
, ,若
,若 ,
, ,
, ,要使
,要使 ,则应增加的条件是
,则应增加的条件是  B.
B. C.
C.  D.
D.
 的不等式:
的不等式: 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2. 的值;
的值; ,若
,若 ,求
,求 的最大值
的最大值 、
、 、
、 三项活动,且每项活动有且仅有1人参加,甲不参加
三项活动,且每项活动有且仅有1人参加,甲不参加 活动,则不同的选派方法有 种.
活动,则不同的选派方法有 种. 满足
满足 ,若
,若 则
则 ( )
( )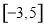 上随机取一个数
上随机取一个数 ,则使函数
,则使函数 无零点的概率是 .
无零点的概率是 .
 中,已知动圆过点
中,已知动圆过点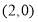 ,且被
,且被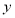 轴所截得的弦长为4.
轴所截得的弦长为4.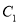 的方程;
的方程;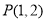 分别作斜率为
分别作斜率为 的两条直线
的两条直线 ,交
,交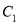 于
于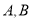 两点(点
两点(点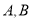 异于点
异于点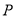 ),若
),若 ,且直线
,且直线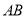 与圆
与圆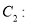
 相切,求△
相切,求△ 的面积.
的面积.