题目内容
已知定义域为 的单调函数
的单调函数 ,若对任意的
,若对任意的 ,都有
,都有 ,则方程
,则方程 的解的个数是
的解的个数是
A.0 B.1 C.2 D.3
B
【解析】
试题分析:根据题意,对任意的 ,都有
,都有 ,即
,即 ,又由
,又由 是定义在
是定义在 上的单调函数,则
上的单调函数,则 为定值,设
为定值,设 ,则
,则 ,又由
,又由 ,即
,即 ,解可得,
,解可得, ;则
;则 , 在同一坐标系内做出函数
, 在同一坐标系内做出函数 与函数
与函数 的图像,如下图:
的图像,如下图:

可得方程 的解的个数是1个.
的解的个数是1个.
考点:1.根的存在性及根的个数判断;2.对数函数图象与性质的综合应用.

练习册系列答案
相关题目
(本小题满分12分)某校在一次对学生在课外活动中喜欢跑步和喜欢打球的学生的抽样调查中,随机抽取了100名同学,相关数据如下表所示:
喜欢跑步 | 喜欢打球 | 总计 | |
男生 | 23 | 32 | 55 |
女生 | 29 | 16 | 45 |
总计 | 52 | 48 | 100 |
(1)由表中数据直观分析,喜欢打球的学生是否与性别有关?
(2)用分层抽样的方法在喜欢打球的学生中随机抽取6名,男学生应该抽取几名?
(3)在上述抽取的6名学生中任取2名,求恰有1名女学生的概率.
 与
与 相交于点
相交于点 、
、 两点,则
两点,则 ______.
______. ∈P C.(
∈P C.( i)2∈P D.
i)2∈P D. ∈P
∈P ,若
,若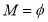 ,则实数
,则实数 的取值范围是_______________ .
的取值范围是_______________ . 
 上是减函数
上是减函数 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,则角
,则角 ________.
________. 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 在点
在点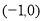 处取得最大值,则实数
处取得最大值,则实数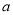 的取值范围为_________.
的取值范围为_________. ,假定
,假定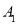 正面向上的概率为
正面向上的概率为 ,
,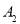 正面向上的概率为
正面向上的概率为 ,
, 正面向上的概率为t(0<t<1),把这三枚金属制品各抛掷一次,设
正面向上的概率为t(0<t<1),把这三枚金属制品各抛掷一次,设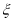 表示正面向上的枚数。
表示正面向上的枚数。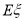 (用t表示);
(用t表示);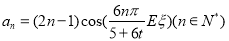 ,求数列
,求数列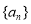 的前n项和.
的前n项和.