题目内容
已知二次函数满足f（x+1）-f（x）=2x，且f（0）=1，求f（x）的解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：要求二次函数的解析式，利用直接设解析式的方法，一定要注意二次项系数不等于零，在解答的过程中使用系数的对应关系，解方程组求的结果．
解答：
解：设二次函数的解析式为f（x）=ax2+bx+c （a≠0）
由f（0）=1得c=1，
故f（x）=ax2+bx+1．
因为f（x+1）-f（x）=2x，
所以a（x+1）2+b（x+1）+1-（ax2+bx+1）=2x．
即2ax+a+b=2x，
根据系数对应相等
∴
所以f（x）=x2-x+1
由f（0）=1得c=1，
故f（x）=ax2+bx+1．
因为f（x+1）-f（x）=2x，
所以a（x+1）2+b（x+1）+1-（ax2+bx+1）=2x．
即2ax+a+b=2x，
根据系数对应相等
|
∴
|
所以f（x）=x2-x+1
点评：本题利用的知识点的较少，直接设解析式，利用方程组求解
练习册系列答案
相关题目
已知x，y，z∈R+，且x+4y+9z=1，则
+
+
的最小值是（ ）
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| A、9 | B、16 | C、36 | D、81 |
某中学团委组织了“弘扬奥运精神，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后画出如图所示部分频率分布直方图．观察图形给出的信息，回答下列问题：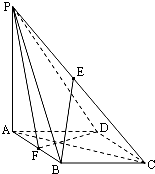
如图在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=PA=2，PA⊥平面ABCD，E是PC的中点，F是AB中点．