题目内容
(本题满分12分)本题共2小题,第(1)小题6分,第(2)小题6分.
如图所示,在长方体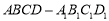 中,
中,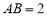 ,
,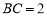 ,
,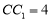 ,
,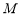 为棱
为棱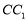 上一点.
上一点.

(1)若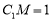 ,求异面直线
,求异面直线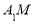 和
和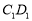 所成角的正切值;
所成角的正切值;
(2)若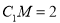 ,求证
,求证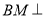 平面
平面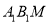 .
.
(1) ,(2)证明略,
,(2)证明略,
【解析】
试题分析:第一步首先找到异面直线 和
和 所成角,由于
所成角,由于 ,则锐角
,则锐角 为异面直线
为异面直线 和
和 所成角,在直角三角形
所成角,在直角三角形 中求出
中求出 ,当然也可以建立空间直角坐标系,用向量的方法去求;第二步证明线面垂直,先寻求线线垂直,首先
,当然也可以建立空间直角坐标系,用向量的方法去求;第二步证明线面垂直,先寻求线线垂直,首先 ,而证明
,而证明 可采用数据计算,看是否满足勾股定理,
可采用数据计算,看是否满足勾股定理, ,,
,, ,恰好满足勾股定理,当然本部证明若使用空间向量更简单.
,恰好满足勾股定理,当然本部证明若使用空间向量更简单.
试题解析:(1)由题意, ,
, ,得
,得
 ,所以异面直线
,所以异面直线 和
和 所成角即为
所成角即为 和
和 所成角,长方体
所成角,长方体 中,
中, ,
, 面
面 ,
, ,故可得
,故可得 为锐角且
为锐角且
(2)由题意, ,
, ,
,

 ,
, ,即
,即 ,又由
,又由 面
面 可得
可得 ,故
,故 平面
平面 .
.
考点:1.异面直线所成的角;2.线面垂直;

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
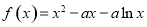 (
(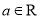 ).
).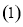 若函数
若函数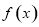 在
在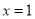 处取得极值,求
处取得极值,求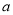 的值;
的值; 在
在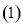 的条件下,求证:
的条件下,求证: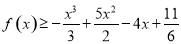 ;
;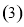 当
当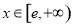 时,
时,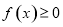 恒成立,求
恒成立,求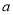 的取值范围.
的取值范围.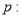 函数
函数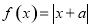 在
在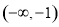 上是单调函数,
上是单调函数,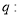 函数
函数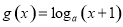 (
(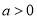 且
且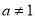 )在
)在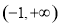 上是增函数,则
上是增函数,则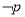 成立是
成立是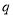 成立的( )
成立的( )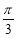 ,a+b与b的夹角为
,a+b与b的夹角为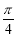 ,则
,则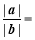 ( )
( )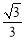 (B)
(B)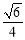
 (D)
(D)
 是纯虚数,则实数m的值为( )
是纯虚数,则实数m的值为( ) (D)
(D)
 和
和 取遍所有实数时,
取遍所有实数时, 恒成立,则
恒成立,则 的最小值为 .
的最小值为 .  的反函数为
的反函数为 ,如果函数
,如果函数 ,那么函数
,那么函数 的图像一定过点 .
的图像一定过点 .  ,
, __________.
__________.
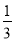 C.
C.  D.
D. 