题目内容
当 和
和 取遍所有实数时,
取遍所有实数时, 恒成立,则
恒成立,则 的最小值为 .
的最小值为 .

【解析】
试题分析:首先把题目中的字母更改一下,当 和
和 取遍所有实数,
取遍所有实数,
这时设 ,令
,令 ,则点
,则点 的轨迹为直线
的轨迹为直线 ;设
;设 ,令
,令 ,则点
,则点 的轨迹为圆
的轨迹为圆 在第一象限的四分之一圆弧,而
在第一象限的四分之一圆弧,而 表示圆弧上一点与直线上一点的距离的平方,画出图形可以看出,当取圆弧上一点
表示圆弧上一点与直线上一点的距离的平方,画出图形可以看出,当取圆弧上一点 时,点
时,点 到直线
到直线 的距离最小,此时
的距离最小,此时 ,
,
 取最大值为8,要使当
取最大值为8,要使当 和
和 取遍所有实数时,
取遍所有实数时, 恒成立,则
恒成立,则 的最小值为
的最小值为 .
.
考点:1.直线和圆的参数方程;2.两点间的距离;

练习册系列答案
相关题目
 为偶函数且
为偶函数且 ,又
,又 ,函数
,函数 ,若
,若 恰好有2个零点,则
恰好有2个零点,则 .
.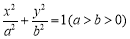 的焦距为
的焦距为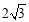 ,且经过点
,且经过点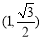 .
.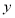 轴正半轴的交点, 椭圆Ω上是否存在两点M、N,使得△AMN是以A为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
轴正半轴的交点, 椭圆Ω上是否存在两点M、N,使得△AMN是以A为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.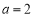 ”是“直线
”是“直线 和
和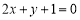 互相平行”的 ( )
互相平行”的 ( )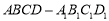 中,
中,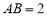 ,
,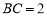 ,
,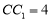 ,
,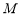 为棱
为棱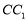 上一点.
上一点.
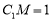 ,求异面直线
,求异面直线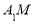 和
和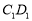 所成角的正切值;
所成角的正切值;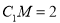 ,求证
,求证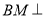 平面
平面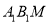 .
. 的动弦
的动弦 的长为
的长为 ,则弦
,则弦 到
到 轴的最短距离是 .
轴的最短距离是 .  是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 .
.  ,则黄豆落入阴影部分的概率为( )
,则黄豆落入阴影部分的概率为( )




 ,
,  B.
B.  C.
C.  D.
D. 