题目内容
(本小题满分12分)已知函数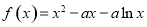 (
(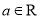 ).
).
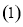 若函数
若函数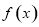 在
在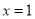 处取得极值,求
处取得极值,求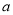 的值;
的值;
 在
在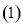 的条件下,求证:
的条件下,求证: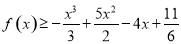 ;
;
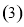 当
当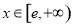 时,
时,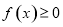 恒成立,求
恒成立,求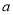 的取值范围.
的取值范围.
(1)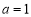 ;(2)详见解析;(3)
;(2)详见解析;(3)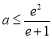 .
.
【解析】
试题分析:(1)显然首先求导可得: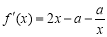 ,利用导数与函数极值的关系可得
,利用导数与函数极值的关系可得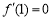 ,解得
,解得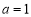 ,经检验,
,经检验,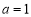 时
时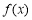 在
在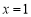 处取得极值,所以
处取得极值,所以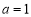 ;(2)根据题意可得由(1)已知:
;(2)根据题意可得由(1)已知: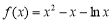 ,可令一新函数
,可令一新函数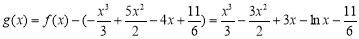 ,观察它的特点,易得要利用导数与函数的关系进行处理,即:
,观察它的特点,易得要利用导数与函数的关系进行处理,即: ,可知
,可知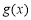 在
在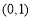 上是减函数,在
上是减函数,在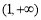 上是增函数,所以
上是增函数,所以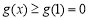 ,所以
,所以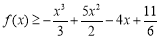 成立;(3)由
成立;(3)由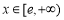 知,
知,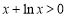 ,采用参数分离的方法可得:
,采用参数分离的方法可得: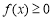 恒成立等价于
恒成立等价于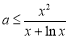 在
在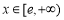 时恒成立,又令一新函数
时恒成立,又令一新函数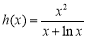 ,
,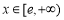 ,有
,有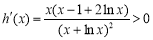 ,所以
,所以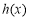 在
在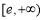 上是增函数,有
上是增函数,有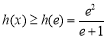 ,所以可求得:
,所以可求得: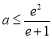 .
.
试题解析:(1)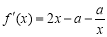 ,由题意可得
,由题意可得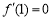 ,解得
,解得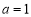
经检验,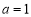 时
时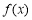 在
在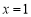 处取得极值,所以
处取得极值,所以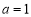 (3分)
(3分)
(2)证明:由(1)知,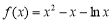
令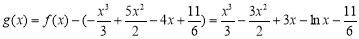
由 ,
,
可知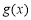 在
在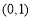 上是减函数,在
上是减函数,在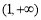 上是增函数
上是增函数
所以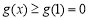 ,所以
,所以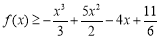 成立 (8分)
成立 (8分)
(3)由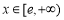 知,
知,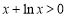
所以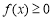 恒成立等价于
恒成立等价于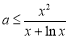 在
在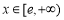 时恒成立
时恒成立
令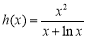 ,
,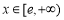 ,有
,有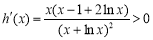 ,
,
所以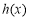 在
在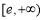 上是增函数,有
上是增函数,有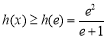 ,所以
,所以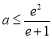 . (12分)
. (12分)
考点:1.利用导数研究函数的单调性;2. 利用导数研究函数的极值

练习册系列答案
相关题目
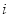 是虚数单位,若复数
是虚数单位,若复数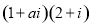 是纯虚数,则实数
是纯虚数,则实数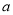 等于( )
等于( )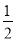 C.
C.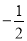 D.
D.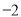
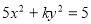 的一个焦点是(0,2),那么
的一个焦点是(0,2),那么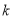 等于 ( )
等于 ( ) C.1 D.
C.1 D.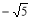
 的大致图像是( )
的大致图像是( ) 
 的终边过点
的终边过点 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 为偶函数且
为偶函数且 ,又
,又 ,函数
,函数 ,若
,若 恰好有2个零点,则
恰好有2个零点,则 .
. ,若其图象是由
,若其图象是由 图象向左平移
图象向左平移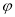 (
( )个单位得到,则
)个单位得到,则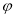 的最小值为( )
的最小值为( )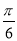 B.
B. C.
C.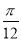 D.
D.
 为偶函数且
为偶函数且 ,又
,又 ,函数
,函数 ,若
,若 恰好有4个零点,则
恰好有4个零点,则 的取值范围是 .
的取值范围是 .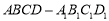 中,
中,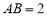 ,
,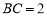 ,
,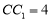 ,
,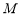 为棱
为棱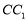 上一点.
上一点.
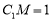 ,求异面直线
,求异面直线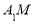 和
和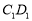 所成角的正切值;
所成角的正切值;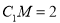 ,求证
,求证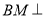 平面
平面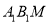 .
.