题目内容
13.在△ABC中,$cosA=\frac{4}{5}$,则$sin(A+\frac{π}{4})$=$\frac{7\sqrt{2}}{10}$.分析 由条件利用同角三角函数的基本关系,两角差的正弦公式,求得$sin(A+\frac{π}{4})$的值.
解答 解:△ABC中,$cosA=\frac{4}{5}$,∴sinA=$\frac{3}{5}$,则$sin(A+\frac{π}{4})$=sinAcos$\frac{π}{4}$+cosAsin$\frac{π}{4}$=$\frac{3}{5}•\frac{\sqrt{2}}{2}$+$\frac{4}{5}•\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{10}$,
故答案为:$\frac{7\sqrt{2}}{10}$.
点评 本题主要考查同角三角函数的基本关系,两角差的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
18.函数y=-x2+4x-2,x∈[0,4)的值域是( )
| A. | (-2,2) | B. | [-2,2] | C. | [0,3] | D. | [-2,0] |
5.下列转化结果错误的是( )
| A. | 67°30′化成弧度是$\frac{3}{8}$π | B. | -$\frac{10}{3}$π化成度是-600° | ||
| C. | -150°化成弧度是$\frac{5}{6}$π | D. | $\frac{π}{12}$化成度是15° |
2.“(2x-1)x=0”是“x=0”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
3.下列各图中,不可能表示函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
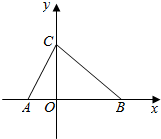 如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$
如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$