题目内容
22.设正整数数列{an}满足:a2=4,且对于任何n∈N*,有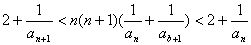 .
.(1)求a1,a3;
(2)求数列{ an }的通项an .
解:(1)据条件得![]() ①
①
当n=1时,由![]() ,即有
,即有![]() ,
,
解得![]() ,因为a1为正整数,故a1=1.
,因为a1为正整数,故a1=1.
当n=2时,由![]() ,解得8<a3<10,所以a3=9.
,解得8<a3<10,所以a3=9.
(2)方法一:由a1=1,a2=4,a3=9,猜想:an=n2
下面用数学归纳证明.
![]() 当n=1,2时,由(1)知an=n2均成立;
当n=1,2时,由(1)知an=n2均成立;
![]() 假设
假设![]() 成立,即ak=k2,则n=k+1时
成立,即ak=k2,则n=k+1时
由①得![]()
![]()
![]()
因为![]() 时,(k3+1)-(k+1)2=k(k+1)(k-2)
时,(k3+1)-(k+1)2=k(k+1)(k-2)![]() 0.所以
0.所以![]() 。
。
k-1![]() 1,所以
1,所以![]()
又![]() ,所以
,所以![]()
故ak+1=(k+1)2,即n=k+1时,an=n2成立。
由![]() ,
,![]() 知,对任意
知,对任意![]() ,an=n2.
,an=n2.
(2)方法二:
由a1=1,a2=4,a3=9, 猜想:an=n2
下面用数学归纳法证明.
![]() 当n=1,2时,由(1)知an=n2均成立;
当n=1,2时,由(1)知an=n2均成立;
![]() 假设
假设![]() 成立,即ak=k2,则n=k+1时
成立,即ak=k2,则n=k+1时
由①得![]()
即![]() ②
②
由②左式,得![]() ,即(k-1)ak+1<k3+k2-k,因为两端为整数,
,即(k-1)ak+1<k3+k2-k,因为两端为整数,
则(k-1)ak+1![]() k3+k2-k-1=(k+1)2(k-1).于是ak+1
k3+k2-k-1=(k+1)2(k-1).于是ak+1![]() (k+1)2 ③
(k+1)2 ③
又由②右式,![]() ,
,
则(k2-k+1)ak+1>k3(k+1).
因为两端为正整数,则(k2-k+1)ak+1![]() k4+k3+1,
k4+k3+1,
所以![]() 。
。
又因![]() ,ak+1为正整数,则
,ak+1为正整数,则![]() ④
④
据③④ak+1=(k+1)2,即n=k+1时,an=n2成立.
由![]() 、
、![]() 知,对任意
知,对任意![]() ,
,![]() .
.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
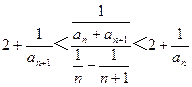 .
.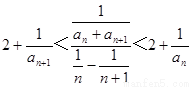 .
.