题目内容
设正整数数列{an}满足:a2=4,且对于任何n∈N*,有2+
<
<2+
,则a10=
| 1 |
| an+1 |
| ||||
|
| 1 |
| an |
100
100
.分析:利用2+
<
<2+
,代入计算,可得结论.
| 1 |
| an+1 |
| ||||
|
| 1 |
| an |
解答:解:∵2+
<
<2+
,a2=4,
∴n=1时,2+
<
+
<2+
,解得
<a1<
.
∵a1为正整数,∴a1=1.
当n=2时,由2+
<6(
+
)<2+
,解得8<a3<10,所以a3=9.
同理可得a4=16;a5=25;a6=36;a7=49;a8=64;a9=81;a10=100.
故答案为:100
| 1 |
| an+1 |
| ||||
|
| 1 |
| an |
∴n=1时,2+
| 1 |
| 4 |
| 2 |
| a1 |
| 2 |
| 4 |
| 1 |
| a1 |
| 2 |
| 3 |
| 8 |
| 7 |
∵a1为正整数,∴a1=1.
当n=2时,由2+
| 1 |
| a3 |
| 1 |
| 4 |
| 1 |
| a3 |
| 1 |
| 4 |
同理可得a4=16;a5=25;a6=36;a7=49;a8=64;a9=81;a10=100.
故答案为:100
点评:本题考查不等式,考查赋值法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
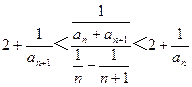 .
.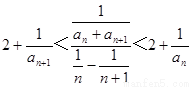 .
.